Regresión y ajuste de la recta
Muy a menudo, en el lenguaje diario, usamos sin darnos cuenta los términos correlación y regresión. Intentamos predecir o averiguar si dos variables tienen relación entre ellas, o si a través de una podemos explicar la otra.
- Encontrar si dos variables tienen relación entre ellas (cualquiera que sea), es lo que denominamos correlación.
- Intentar explicar una de ellas, a partir de la otra, es lo que conocemos como regresión.
Antes de iniciar el estudio de estas técnicas, debemos explicar qué es una variable dependiente y una independiente. Lo veremos con dos ejemplos.
- El número de lechones destetados por cerda y año es función de la fertilidad de la granja, luego la fertilidad es la variable independiente y el número de lechones es la variable dependiente (depende de la fertilidad).
- El número de lechones destetados por cerda y año es función de la mortalidad perinatal. Por lo tanto, la mortalidad perinatal es la variable independiente, y el número de lechones la variable dependiente (depende de la mortalidad perinatal). Pero ni la mortalidad perinatal es función de la fertilidad, ni viceversa, aunque puedan estar relacionadas (por ejemplo, si un proceso infeccioso afecta a la granja).
Un concepto que no debemos confundir es el de causalidad. El hecho de que exista correlación, o que realicemos un análisis de regresión entre los variables, no implica que haya una relación de causa-efecto o causalidad entre estas dos variables. Esta relación de causa-efecto debemos establecerla nosotros con criterios biológicos, técnicos, bibliográficos …
En este artículo explicamos con detalle la regresión y desarrollamos un caso práctico para facilitar su comprensión. Si los lectores desean leer más a fondo en qué consiste la correlación, y un caso práctico, en este artículo lo tenemos publicado.
Regresión
La regresión tiene dos vertientes, una descriptiva (vemos lo que “hay”) y otra inferencial (sacamos conclusiones).
- La vertiente descriptiva, que veremos en este artículo, nos permitirá estudiar la relación lineal entre dos variables estableciendo la ecuación de la recta (a partir de ahora la denominaremos recta de regresión) que mejor se ajuste a esos datos y descomponiendo la variabilidad total de la variable dependiente en dos partes: la parte de la variabilidad total explicada por la recta de regresión a partir de la variable independiente y la parte no explicada (también llamada residual), y que nos sirve para evaluar el ajuste de la recta. Veremos en el próximo artículo cómo explicar la variabilidad total así de una forma gráfica.
- La vertiente inferencial supone que los datos que vamos a estudiar son una muestra al azar, y permitirá evaluar si en la población las variables están relacionadas. En caso afirmativo, podremos estimar la recta de regresión que mejor predice un caso de la variable dependiente de esa población a partir del valor conocido de un caso de la variable independiente.
Recta de regresión
Hemos intentado evitar las explicaciones y las demostraciones matemáticas de lo explicado a continuación. Sin embargo, en la regresión nos parece fundamental comprender el mecanismo matemático, ya que a través de su conocimiento podremos entender perfectamente el estudio de la regresión lineal, que nos servirá para explicar más adelante el modelo general lineal que es usado para la mayor parte de los experimentos en ciencias de la salud.
Lo primero que vamos a hacer es explicar cómo, a través de una serie de datos, obtenemos una recta de ajuste, la recta de regresión. Para ello recordaremos primero el concepto de ecuación de una recta y el significado de sus coeficientes. La ecuación de una recta viene dada por la fórmula: y = a + bx, donde a y b son los coeficientes de la recta:
■ a indica el valor para el punto x = 0, que es el punto de corte de la recta con el eje de ordenadas (eje y). Si tomamos x = 0 , entonces bx = 0 e y = a;
■ b indica la pendiente de la recta, es decir, el incremento de y por cada unidad que se incrementa x. Si tomamos a = 0 y x = 1, entonces y = b. y donde x e y son los valores de las variables:
- y es el valor para la variable dependiente, es decir, la explicada.
- x es el valor para la variable independiente, es decir, la que explica.
Si lo vemos de una forma gráfica es muy fácil de entender (figura 1).
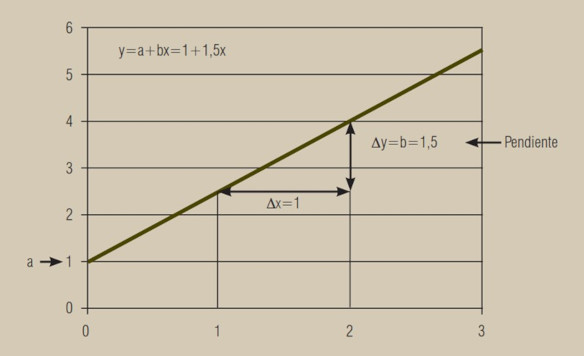
En la recta, el valor a = 1 indica el punto de corte de la recta con el eje de ordenadas y el valor b = 1,5 indica el incremento de la variable y por cada unidad que se incrementa la variable x. La recta de regresión es por lo tanto y = a + bx = 1 + 1,5x.
Criterio de ajuste de la recta de regresión
Y ¿cómo ajustamos una recta a una nube de puntos? ¿Qué criterio vamos a seguir? Lo veremos con las mínimas expresiones matemáticas y con una serie de gráficos.
Imaginemos el gráfico siguiente:
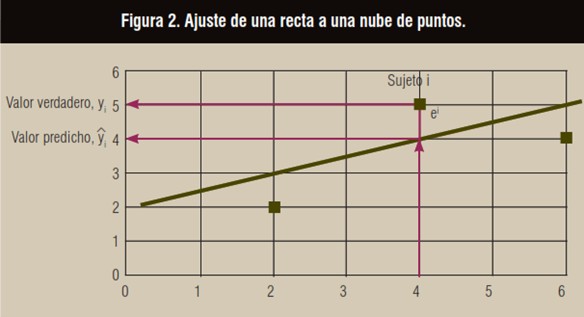
Si trazásemos una recta para describir estos tres puntos, podríamos decir que la recta que aparece describiría bastante bien, al menos desde un punto visual, los tres puntos. Debido a la variabilidad de los datos, si se utiliza esta recta para predecir el valor yi de un sujeto i en función de su valor xi, se observa que hay una diferencia ei llamada residual, que representa el error de predicción:
ei = yi – yi.
El criterio de ajuste de la recta debe minimizar el conjunto de residuales ei. Podría pensarse en hacer mínimo la suma del valor absoluto de los residuales pero esta condición conduce a un ajuste muy insatisfactorio. La solución generalmente adoptada es minimizar la suma de los residuales al cuadrado, porque este criterio tiene una fácil solución matemática y produce ajustes correctos en la mayor parte de situaciones.
Vamos a verlo de una forma empírica y no con una resolución matemática.
En la figura siguiente tenemos un gráfico con los mismos puntos de la figura 2, pero con dos líneas de ajuste diferentes: una granate y una verde.
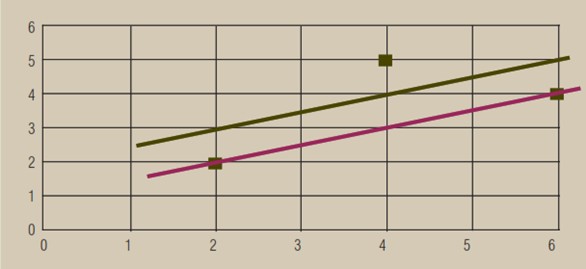
Las ecuaciones de estas dos rectas son:
Recta granate: y = 0,5x
Recta verde: y = 2 + 0,5x
¿Cuál de las dos rectas explica mejor la relación entre x e y? Recordamos que hemos hablado de tres criterios: vamos a ver qué recta se elegiría en cada caso y con cuál de las dos rectas (y con qué criterio) nos quedamos:
■ Si seguimos un criterio “intuitivo” podemos elegir al responder a la pregunta ¿cuál ajusta visualmente mejor?
■ Si seguimos el criterio ¿cuánto vale la suma de los valores absolutos de los residuales en cada una de las dos rectas? Tenemos que hacer estas sumas:
- Recta granate: ei = 0 + 2 + 0 = 2
- Recta verde: ei = 1 + 1 + 1 = 3
■ Por último seguimos este criterio: ¿cuánto vale la suma de residuales al cuadrado de cada recta?
- Recta granate: ei = 02 + 22 + 02 = 4
- Recta verde: ei = 12 + 12 + 12 = 3
Elección de la recta
El lector observará que la recta granate tiene dos residuales nulos y un residual igual a 2, mientras que la recta verde tiene todos sus residuales iguales a 1. En valor absoluto, la suma de residuales es mayor en la recta verde que en la granate, pero al elevar los residuales al cuadrado, la suma es menor en la recta verde que en la granate.
El motivo de elevar los residuales al cuadrado es porque las grandes diferencias se magnifican y el ajuste de mínimos cuadrados busca una recta de compromiso que evite residuales muy grandes. Esta propiedad tiene como consecuencia que la recta estimada matemáticamente tienda a coincidir con la que ajustaría el ojo humano. Nos quedamos con el criterio de los mínimos cuadrados (opción c).
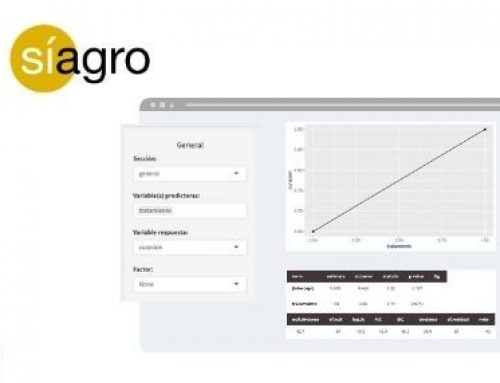
Un ejemplo con Síagro
Visto ya el fundamento matemático, aunque lo hayamos desarrollado de forma empírica, vamos a ver cómo realizar la regresión con Síagro.
Suponiendo que tenemos de partida los siguientes datos:
| Cerdo | CMD | GMD |
| 1 | 1.064 | 532 |
| 2 | 1.168 | 556 |
| 3 | 905 | 411 |
| 4 | 1.124 | 562 |
| 5 | 1.100 | 523 |
| 6 | 1.198 | 544 |
| 7 | 935 | 467 |
| 8 | 1.088 | 518 |
| 9 | 1.109 | 554 |
| 10 | 1.009 | 438 |
Para estudiar la regresión entre la Ganancia Media Diaria GMD (variable dependiente) y el Consumo Medio Diario CMD (variable independiente), sólo necesitamos acceder desde el panel de control a Modelos de Predicción / Lineal y seleccionar nuestras variables. Así de sencillo, la aplicación nos devolverá la siguiente salida:
| term | estimate | std.error | statistic | p.value | Sig | ||||||||||||
| (Intercept) | -23,0443 | 97.7 | -0.236 | 0.819 | |||||||||||||
| CMD | 0.4986 | 0.091 | 5.48 | 0.000588 | *** | ||||||||||||
| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs | ||||||
| 0.79 | 0.763 | 25.9 | 30 | 0.000588 | 1 | -45.6 | 97.2 | 98.1 | 5.36e+03 | 8 | 10 | ||||||
De momento sólo vamos a explicar algunos de los datos que aparecen en esta salida, dejando una amplia explicación para el próximo número. ¿Cuál sería la ecuación de nuestra recta de regresión? Recordemos que en nuestro caso la variable y es y = GMD y la variable x es x = CMD.
GMD = -23,0443 + 0,4986 CMD
Es decir, los coeficientes estimados de a y b son lo que Síagro (y R) denomina Estimate. De la ecuación anterior podemos decir que por cada unidad de CMD, la GMD aumenta 0,4986.
Pero una pregunta que nos podemos hacer es ¿realmente podemos confiar en esa relación? O de otra manera: ¿es el coeficiente b diferente de 0? Esta pregunta supone pasar de la descripción a la inferencia, tal y como decíamos al principio del artículo, y se responde con un test t con hipótesis nula b = 0 y alternativa b ≠ 0.
En este caso, el valor p es menor que 0,05 (p-value: 0.000588) y, por tanto, rechazamos la hipótesis nula, o sea que b es diferente de 0. También podemos decir que el CMD explica el 78,96 % de GMD. Pero esto y las explicaciones de la variabilidad, lo veremos en el próximo artículo.