Regresión logística simple: ¿con qué tratamiento tendremos una mayor probabilidad de animales curados?
En este número vamos a abordar una técnica de regresión que nos permite relacionar una variable dependiente categórica (por ejemplo: curados/no curados) con una o más variables independientes cuantitativas y/o categóricas. Se trata de la regresión logística simple.
Para tener un primer contacto con esta técnica de análisis, nos centraremos en la regresión logística binaria simple, que relaciona una variable dependiente dicotómica (dos opciones) y una variable independiente.
¿En qué consiste la regresión logística?
El objetivo de esta técnica estadística es expresar la probabilidad de que ocurra un hecho como función de ciertas variables, que se consideran potencialmente influyentes. Tendremos una variable dependiente categórica, que puede ser dicotómica o politómica y una o más variables independientes cuantitativas y/o categóricas.
Una variable dependiente dicotómica sólo tiene dos posibles respuestas: sí o no, verdadero o falso, enfermo o no enfermo, curado o no curado, éxito o fracaso… Estas respuestas se codifican con valor 1 si ocurre un determinado suceso o con el valor 0 si no ocurre este suceso. Este aspecto de la codificación de las variables no es banal, influye en la forma en que se realizan los cálculos matemáticos y debemos tenerlo en cuenta a la hora de interpretar los resultados.
Por otro lado, este tipo de proceso en el que sólo hay dos resultados posibles (0/1), siendo la probabilidad de cada resultado constante en una serie de repeticiones, se distribuye bajo la ley binomial.
El problema y solución mediante una regresión logística simple
Veamos con un ejemplo práctico cómo plantear e interpretar un modelo de regresión logística simple.
Vamos a comprobar la eficacia de dos tratamientos alternativos sobre la curación de una enfermedad.
El objetivo es estudiar si el proceso curación/no curación está asociado, o no, con el tratamiento. Es decir, si la probabilidad de curación aplicando el tratamiento A es igual, o distinta, a la probabilidad de curación aplicando el tratamiento B.
Para ello, supongamos que hemos realizado un experimento sobre una muestra aleatoria de 40 animales enfermos, divididos aleatoriamente en dos grupos de 20 animales, a cada uno de los cales de le suministra un tratamiento (A o B). Los resultados obtenidos en el experimento se muestran en la siguiente tabla:
| Tratamiento A (X = 1) | Tratamiento B (X = 0) | |
|---|---|---|
| Curación (Y = 1) | 18 | 13 |
| No curación (Y = O) | 2 | 7 |
Antes de plantear un modelo de regresión logística, podemos hacer una serie de cálculos
Podemos estimar la probabilidad de curación (p) para ambos tratamientos:
- Tratamiento B (0,65): p | (X = 0) = 13/20;
- Tratamiento A (0,90): p | (X = 1) = 18/20
En la expresión: p | (X = 0) = 13/20 p es la probabilidad de curación.
| es un símbolo que quiere decir “condicionado a”.
X = 0 indica que los datos pertenecen a los animales asignados al tratamiento B.
Por tanto, la probabilidad de curación para los animales que recibieron el tratamiento B es de un 65 %.
Como ambas probabilidades son numéricamente distintas se podría pensar que la probabilidad de curación depende del tratamiento. Pero antes de llegar a esta conclusión, deberíamos plantearnos dos cuestiones: ¿esta dependencia es generalizable (“estadísticamente significativa”)? y ¿cuánto depende la respuesta del tratamiento (“clínicamente relevante”)?
En este ejemplo la segunda pregunta la podríamos resolver también a partir de los datos de la tabla aplicando los conceptos de odds y odds ratio que explicamos en los artículos de estudios de casos y controles en epidemiología:
- Odds con el tratamiento B = (13/20)/(7/20). Aplicando el tratamiento B hay 1,857 veces más posibilidades de curación que de no curación
- Odds con el tratamiento A = (18/20)/(2/20)). Aplicando el tratamiento A hay nueve veces más posibilidades de curación que de no curación
- Odds ratio OR = odds.tratamiento.B/odds. tratamiento.A. Aplicando el tratamiento A hay 4,846 (≈5) veces más posibilidades de curación que con el tratamiento B
En caso de no haber diferencias, odds y OR valen 1. Aunque recordemos que estos valores son estimaciones puntuales y por lo tanto debemos acompañarlas de su intervalo de confianza para indicar la precisión de la estimación. Por lo que, por el momento, no podemos concluir que la probabilidad de curación dependa del tratamiento (pero sí que vemos la necesidad de estudiarlo con detenimiento).
Regresión logística simple con Síagro
Para realizar este análisis, hemos utilizado el software Síagro y una base de datos con la siguiente información:
| id | curacion | tratamiento |
| 1 | 1 | 0 |
| 2 | 1 | 0 |
| 3 | 1 | 0 |
| . | . | . |
| . | . | . |
| . | . | . |
| 38 | 1 | 1 |
| 39 | 0 | 1 |
| 40 | 0 | 1 |
Lo primero que hemos hecho ha sido iniciar sesión en la aplicación, cargar nuestro fichero Excel y acceder en el panel de control a Modelos de Predicción / Logistica.
Tanto la curación o no curación (variable dependiente) y el tratamiento (variable independiente) son variables que siguen una distribución binomial, pero no tenemos que preocuparnos ni de acordarnos ni de decírselo al software Síagro porque ya lo sabe.
Si seleccionamos nuestras variables en el panel de control:
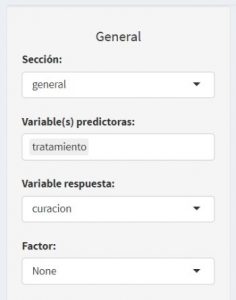
Obtenemos la siguiente salida:
| term | estimate | std.error | statistic | p.value | Sig |
| (Intercept) | 0.619 | 0.469 | 1.32 | 0.187 | |
| tratamiento | 1.58 | 0.88 | 1.79 | 0.0731 | . |
| null.deviance | df.null | logLik | AIC | BIC | deviance | df.residual | nobs |
| 42.7 | 39 | -19.5 | 42.9 | 46.3 | 38.9 | 38 | 40 |
¿Cómo interpretamos esta salida?
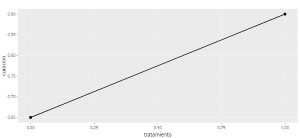
Podemos ver que la salida es bastante similar a las que se obtienen con los modelos de regresión lineal y regresión múltiple. En primer lugar, el gráfico explica la relación entre dos variables y es una línea recta porque se trata de un modelo lineal generalizado.
Estimate: es la estimación de los coeficientes:
- Intercept, origen, es la estimación del coeficiente a (0,6190), que coincide con el logaritmo neperiano de la odds cuando X = 0
- tratamiento es la estimación del coeficiente b (1,578) que es el logaritmo neperiano de OR.
De la misma forma, a partir de los coeficientes a y b podemos calcular la odds cuando X = 0 y el OR sería:
- exp(a)=exp (0,619)= 1,857 = odds para X = 0.
- exp(b)=exp (1,5784)= 4,846 = OR
Std.error: es el error estándar de los coeficientes.
Statistic o Z value: es el estadístico de contraste. Z es la distancia desde la media en relación con la desviación estándar de la media. Se calcula a partir del cociente entre el coeficiente y su error estándar, y permiten obtener el valor-p (Pr(>|z|)) que se muestra a continuación. Igual que en la comparación de medias se utilizaba el test de student y se calculaba un estadístico “t”, para este análisis el estadístico que se usa es el “z”.
p.value (PR(|z|): son los valores de p e indican si los coeficientes son significativamente distintos de cero o no (dado un nivel de significación que establecemos en p<0,05). Hay que tener en cuenta que estudiar si los valores de a y b son significativamente diferentes de 0, o no, equivale a estudiar si exp(a) (odds para el tratamiento B) y exp(b) (OR) son significativamente distintos de 1.
- En el caso del Intercept, Pr (>|z|)=0,187, por lo que no hay significación y no podemos decir que a sea significativamente distinta de cero. En este caso, esta afirmación corresponde también a que exp(a), es decir, la odds para X = 0 (tratamiento B), no es significativamente distinta de 1 (porque exo(0)=1).
Como consecuencia, decimos que para los animales del tratamiento B, la probabilidad de curación es igual a la de no curación.
Del mismo modo, en la fila tratamiento, Pr(>|z|)=0,073; como el nivel de significación es de 0,05, tampoco encontramos significación, así que la conclusión es que exp(b) no es significativamente distinto de 1.
Conclusión: no hay diferencias en cuanto a probabilidad de curación entre los tratamientos A y B.
Como hemos podido comprobar, este software permite a los usuarios obtener un análisis completo y dar respuesta a una pregunta tan compleja en pocos clics.