¿El número de lechones nacidos muertos nos está indicando la aparición de un brote de PRRS?
En este artículo dentro de «Casos de uso de Síagro» lo que vamos a hacer es controlar la evolución de una variable que mide cierta característica de calidad.
Un buen amigo al que hemos introducido en el uso de los gráficos de control para ver la evolución de la producción de su negocio porcino nos ha formulado una pregunta muy interesante. Antes de compartirla, algunos aspectos:
- Partimos de la premisa de que el PRRS modifica el número de lechones nacidos muertos.
- Además, podemos estudiar la variable “nacidos muertos” de diferentes formas: nacidos muertos por parto, totales, en un periodo determinado, habitualmente por semana o como muchos softwares de gestión de granja, como “media de lechones nacidos muertos por parto en una determinada semana”.
Nuestra hipótesis es que el número de lechones nacidos muertos puede indicarnos la aparición de un brote de PRRS. Por tanto, nuestra variable control es: nacidos muertos por parto.
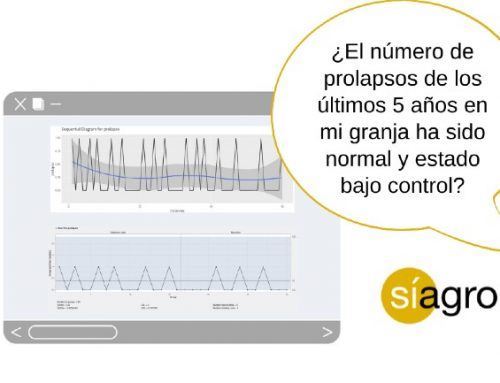
La pregunta: ¿Podríamos ver con gráficos de control pequeños cambios en el número de lechones nacidos muertos que nos avisasen de que quizá ha habido un brote de PRRS y está cambiando su patrón de distribución?
Él ya había intentado realizar varios ejercicios con los gráficos de control, tanto individuales (xbar-one) como con los de rango (en este artículo, explicamos en qué consisten estos gráficos). Lo que veía era que podía detectar cambios en el patrón de comportamiento a largo plazo, pero no a corto.
¿Existe algún método que nos permita controlar la variación a corto plazo y que trabaje tanto con valores individuales como con medias de grupos?
La respuesta: Sí, con los gráficos CUSUM.
Los gráficos CUSUM (de la abreviación inglesa de cumulative sum) se basan en la representación de la acumulación de las desviaciones de cada observación respecto a un valor de referencia. La principal característica de este tipo de gráficos es que detectan pequeñas desviaciones de los datos más rápidamente que los gráficos xbar-one o los gráficos de rango.
Estos gráficos fueron desarrollados por Woodward y Goldsminth en 1964. Lo novedoso de esta técnica es que detecta cambios en las medias de variables, determinando también el punto probable de cuándo el cambio comenzó a realizarse.
Los gráficos CUSUM son menos apropiados para detectar cambios grandes, por lo que son complementarios de los gráficos de media, rango o desviación típica, y no pueden sustituir a los mismos, es decir, debemos usarlos conjuntamente. La idea que subyace en estos gráficos no es una representación individual de valores, como podría ser en este caso para el número de nacidos muertos por parto (dato individual) o promedios del mismo, sino en la acumulación de información en el tiempo. Por ello también se les denomina “gráficos con memoria”.
Cómo construimos un gráfico CUSUM y cómo lo hacemos con el programa Síagro
Sigamos con la pregunta de nuestro amigo y usemos algunos datos, en este caso y por labores didácticas, simulados. Supongamos que tenemos un archivo de datos donde tenemos la media de lechones nacidos muertos por parto durante las últimas 30 semanas (donde cada dato es el porcentaje de la media semanal sobre el total de lechones nacidos):
| semana | muertos |
| 1 | 2,61 |
| 2 | 1,99 |
| 3 | 2,12 |
| 4 | 3,04 |
| . | . |
| . | . |
| . | . |
| 28 | 3,22 |
| 29 | 3,02 |
| 30 | 3,81 |
En primer lugar, cargamos el archivo en Síagro, accedemos a SPC (Control Estadístico de procesos), seleccionamos nuestra variable de interés y obtenemos un gráfico de la media de valores individuales (que el programa nos sugiere realizar al detectar automáticamente el tipo de variable que estamos analizando):
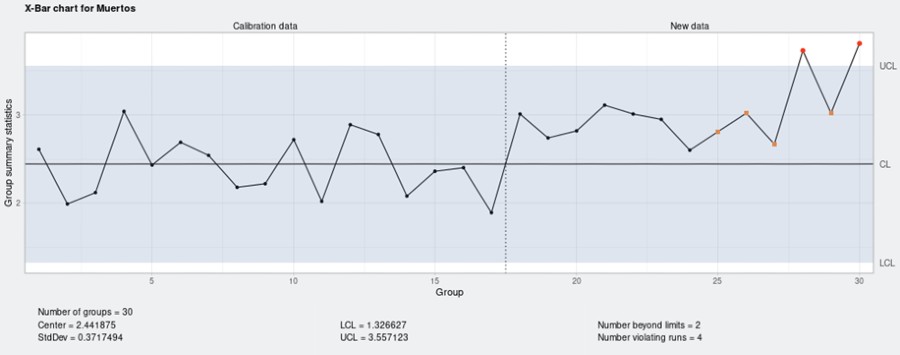
Según el gráfico, el cambio que produjo una primera desviación fuera de control se produjo en la semana 25. Pero veamos qué nos dice un gráfico CUSUM:
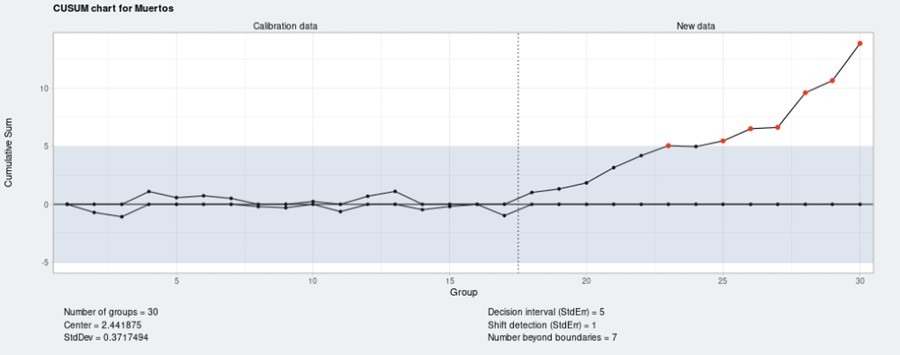
Esto ya cambia.
En este caso, nos está avisando de que se está produciendo un cambio en el valor de nuestra variable a partir de la semana 23.
Si nos centramos en la línea bajo el valor 0, que nos informa de las desviaciones negativas, nos da a entender que hasta la semana 17 los valores eran buenos (teníamos pocos lechones nacidos muertos). Pero a partir de aquí, y sobre todo a partir de la semana 23, el número de lechones muertos se desvía de forma positiva (negativa para nuestros intereses) y sobrepasa el límite de control.
Lo que nos indican las cifras que aparecen en el gráfico es:
- Number of groups = 30; los datos de las 30 semanas.
- Center = 2,441; la media de las 30 semanas.
- StdDev = 0,371; la desviación estándar.
- Decision interval (std.err.) = Los límites de control se fijan a 5 desviaciones por encima y por debajo de la media.
- Shift detection (std.err.) = 1; es el número de desviaciones estándar que aceptamos desde el que queremos detectar desviaciones.
- Number beyond boundaries = 7; puntos que se salen de nuestros límites.
Comparación de gráficos X-bar o I y gráficos CUSUM
Para entender qué partido podemos sacar a los gráficos CUSUM, vamos a compararlos con los gráficos de control X-BAR o I.
Tenemos tres tipos de parámetros: xi, u y di:
- X1, x2, x3, … son las sucesivas observaciones de dicha variable.
- U es el valor objetivo de la variable que queremos controlar. En este caso, u= 2,44.
- D1, d2, d3 … son la sucesión de desviaciones de cada uno de nuestros valores con respecto a la media de referencia u, es decir: d1 = (x1-u) ; d2 = (x2 – u) …
Así:
- Con los gráficos de medias (el primero presentado en el artículo) vemos sencillamente la evolución de los valores con respecto a la media de referencia: d1, d2, d3 …
- Con los gráficos CUSUM, vemos la sucesión de los datos d1, d1+d2, d1+d2+d3 … es decir, se suma la primera desviación de nuestro dato a la desviación del segundo, y así sucesivamente, de forma que cada valor arrastra información de toda la serie de valores y un desajuste pequeño se irá acumulando hasta que lo detectemos. En contraposición, un pequeño desajuste pasará inadvertido en los gráficos de medias X-Bar o I.
| Semana | Lechones nacidos muertos por parto (xi), % | Desviación a nuestro valor objetivo de 2,41% (di) | Acumulación de desviaciones (d1, d1+d2…) |
| 1 | 2,61 | 0,20 | 0,20 |
| 2 | 1,99 | -0,42 | -0,22 |
| 3 | 2,12 | -0,29 | -0,51 |
| 4 | 3,04 | 0,63 | 0,12 |
| … | … | … | … |
* Nos fijamos en el dato de la semana 4, por ejemplo: el valor de la acumulación de desviaciones será el dato de la acumulación para la semana 3 más la desviación propia de la semana 4, es decir: -0.51 + 0.63=0.12.
Como hemos visto en los gráficos, a partir de la semana 17 ya ocurre algo anómalo: todas las acumulaciones de las desviaciones son muy positivas y no paran de crecer.
Con un diagrama secuencial (en Análisis Exploratorio/Secuencial en Síagro) también podemos comenzar a sospechar:
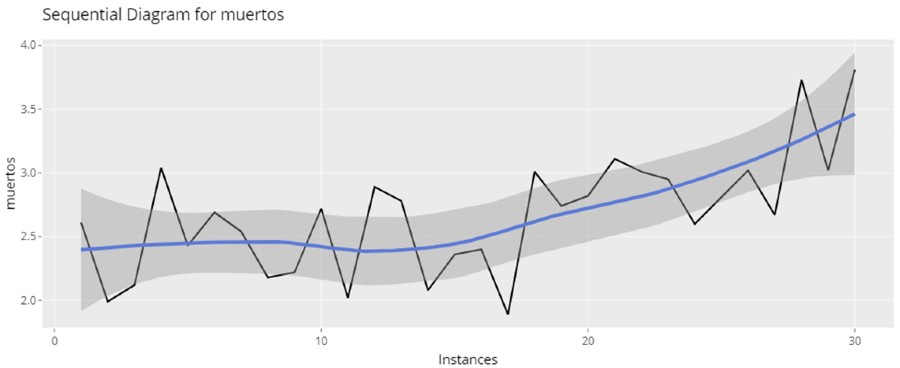
Volviendo al gráfico CUSUM, este gráfico nos distingue ente desviaciones positivas y negativas, ya que no es lo mismo que un valor se desvíe de forma ascendente que descendente para nuestros resultados productivos. Es decir, si una semana o dos de nuestros datos se desvía de forma positiva, es que el número de lechones se incrementa; si se desvía de forma negativa, disminuye.
Cuando la línea está bajo el valor 0, nos informa de las desviaciones negativas y nos da a entender que las semanas donde el valor sube hasta 0, el número de lechones muertos se desvía de forma positiva (negativa para nuestros intereses), y además sobrepasa el límite de control en la semana 30.
Las matemáticas del CUSUM algorítmico
La lógica que subyace en la forma de realizar los cálculos y el gráfico es la siguiente: se define un valor K (que se elige según la desviación que vamos a detectar y que suele ser la mitad de la desviación típica de la variable en la que estamos interesados) a partir del cual consideraremos que la desviación es significativa. Este valor nos dará sensibilidad al gráfico. En la columna de las desviaciones acumuladas consideraremos que la desviación acumulada es 0 si no sobrepasa este valor K. Como a partir de entonces el gráfico sólo nos informará de las desviaciones significativas, y además nos dirá si son positivas o negativas, tendremos un gráfico muy útil.
También tenemos un valor denominado “valor de decisión (H)”, que es el valor con el que se compara nuestra variable y suele ser 5 veces la desviación típica (aunque algunos autores recomiendan usar 4 veces ese valor).
Con el valor H, el valor de decisión y el valor K se calculan los límites de control tanto para la gráfica de desviaciones negativas como de las positivas.