Si el intervalo destete a celo es menor, ¿tenemos mejor fertilidad? Correlación y gráficos de dispersión
¿Qué es la correlación?
La correlación es una medida estadística que expresa cómo se relacionan dos variables de manera lineal, es decir, si cambian conjuntamente de manera constante. Intuitivamente hablamos de que dos variables están correlacionadas cuando existe una relación simétrica entre ellas. No estamos interesados en saber cuál es la variable dependiente y cuál la variable independiente, sino que sólo estudiamos si existe relación entre ellas, así como su sentido.
El ejemplo más evidente puede ser el de comparar el peso y la talla en la población humana, o en el caso de los cerdos, el consumo diario de pienso y el crecimiento diario.
Supongamos que medimos la temperatura del producto del que estamos analizado la merma. Para ver si existe relación entre ambas variables se utilizan los llamados gráficos de dispersión, o nube de puntos, donde cada punto representa el cruce entre los valores de ambas variables: una en el eje horizontal y otra en el eje vertical. En el siguiente gráfico podemos ver que cuando una variable aumenta, la otra también lo hace.
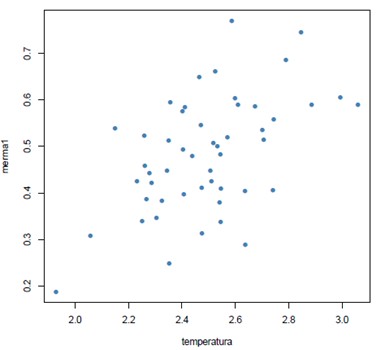
Los datos se muestran como un conjunto de puntos, cada uno con el valor de una variable que determina la posición en el eje horizontal (x) y el valor de la otra variable determinado por la posición en el eje vertical (y).
Las relaciones entre los conjuntos de datos se infieren según la forma de las nubes, de manera que:
- Una relación positiva entre x e y significa que los valores crecientes de x están asociados con los valores crecientes de y.
- Una relación negativa significa que los valores crecientes de x están asociados con los valores decrecientes de y.
Tipos de correlación
- Correlación negativa: Un aumento de x generará una disminución de y. Las variables se producen en dirección opuesta y el coeficiente de correlación (ρ) está entre 0 y -1. Cuando ρ es -1, se dice que la relación está perfectamente correlacionada negativamente.
- Correlación positiva: Un aumento de y depende de un aumento de x. Cuanto más se acerca el valor de ρ a +1, más potente es la relación lineal. Por ejemplo, supongamos que el valor de los precios del pienso está directamente relacionado con los precios de la gasolina (que interviene en el transporte y su coste), con un coeficiente de correlación de +0,95. Cuando más caros son los gastos de transporte, más cara será la compra del pienso.
- Correlación nula (sin correlación): La gráfica no sigue una tendencia, los puntos están totalmente dispersos.
Por ejemplo, si nos encontramos ante una correlación negativa significa que al aumentar el % de materia prima en un determinado pienso, disminuye el número de productos no conformes. Por ello, en base a esta información y aunque deberíamos llevar a cabo un análisis más exhaustivo, ya sabemos que debemos plantearnos utilizar esta nueva materia prima.
Las correlaciones de Pearson con valores por debajo de 0,30 son débiles, pero debemos tener en cuenta también si son o no significativas estadísticamente y su significación biológica.
El siguiente gráfico es un diagrama de dispersión obtenido con Síagro y representa una correlación negativa entre las variables: “Average end parity” y “Number of litters per female mated and year”. Vemos además que nos saca el índice correspondiente:
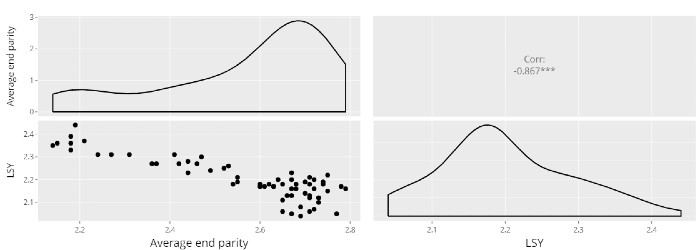
¿Por qué hay dos gráficos? Como hemos dicho, se estudia la relación de dos variables, en los que en el eje X está la variable independiente y en el Y la dependiente. Como en el caso de la correlación no hay relación de dependencia, sino que la mida en dos sentidos, obtenemos dos gráficos.
Caso de uso 1: Correlación de cuatro variables: media del número de lechones nacidos totales, porcentaje de fertilidad a parto, porcentaje de cerdas cubiertas, media del intervalo destete-celo
Vamos a utilizar una base de datos que incluye información de los resultados medios semanales de una granja de cerdas desde 2008 a 2011. Las variables que tiene el archivo son:
- Id: identificador.
- date: fecha.
- avg_totalborn: media del número de lechones nacidos totales correspondientes a las cubricines realizadas durante esa semana.
- fertilidad: porcentaje de fertilidad a parto obtenida en esa semana de cubriciones.
- cedttcub: porcentaje de cerdas cubiertas durante la semana correspondiente de cubriciones transcurridos siete o menos días desde su destete.
- idc: media del intervalo destete-celo de las cerdas cubiertas durante una semana.
Resumen del archivo utilizado para el análisis con Síagro:
| id | date | avg_totalborn | fertilidad | cerdttcub | idc |
| 1 | 01/01/2008 | 13,16 | 54,6 | 76,47 | 11,7 |
| 2 | 08/01/2008 | 13,27 | 54,79 | 81,42 | 10 |
| 3 | 15/01/2008 | 13,65 | 74,3 | 87,76 | 9,1 |
| 4 | 22/01/2008 | 13,32 | 67,53 | 78,12 | 8,2 |
| 5 | 29/01/2008 | 12,97 | 70,75 | 79,81 | 8,3 |
| 6 | 05/02/2008 | 13,3 | 68,33 | 81,98 | 8,1 |
| . | . | . | . | . | . |
| . | . | . | . | ||
| . | |||||
| 208 | 19/12/2011 | 13,24 | 78,22 | 93,08 | 6,2 |
| 209 | 26/12/2011 | 13,35 | 75,49 | 92,55 | 6,8 |
Las preguntas que queremos responder con estos datos son la relación entre las variables:
- “fertilidad” y “cerdttcub”: es decir, si cubrimos más cerdas en los siete días posteriores al destete, ¿tenemos mayor fertilidad?
- “fertilidad” e “idc”: si el intervalo destete a celo es menor, ¿tenemos mejor fertilidad?
- “avg_totalborn” y “fertilidad”: si tenemos mayor fertilidad, ¿tenemos más lechones nacidos totales?
- “avg_totalborn” y “cerdttcub”: si cubrimos más cerdas en los siete días posteriores al destete, ¿tenemos más lechones nacidos totales?
- “idc” y “avg_totalborn”: si el intervalo del destete al celo es menor, ¿tenemos más nacidos totales?
Para estudiar la relación entre las variables mencionadas, podríamos seleccionar cada una de las anteriores relaciones y crear un gráfico de dispersión para cada combinación, con lo que veríamos contestadas nuestras preguntas. Pero … ¿podríamos ver en un solo gráfico las relaciones entre todas ellas a la vez? Síagro nos permite hacer todos estos cruces en un único gráfico y visualizarlo en un gráfico de dispersión, junto con el estadístico de correlación.
Simplemente tenemos que ir a EDA / Pairs y seleccionar en el panel de control de Síagro todas nuestras variables. La salida que obtendríamos sería la siguiente:
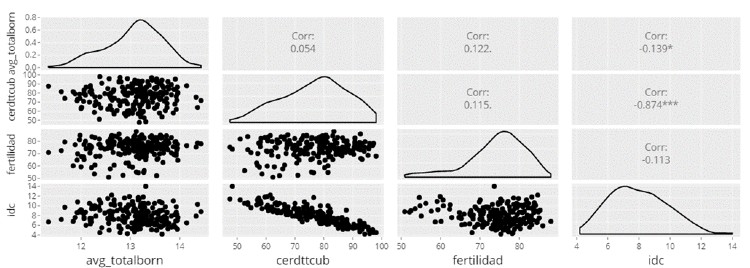
A partir del anterior gráfico y el estadístico de correlación calculado (que nos confirma o no la relación y sentido de las variables, como hemos visto), ya podemos comenzar a extraer conclusiones.
Si nos fijamos en las diferentes tablas, se puede afirmar que:
- Existe una correlación estadísticamente significativa (p<0,05) entre “cerdttcub” e “idc” (elevada y negativa, -0,874, que indicaría que al aumentar “cerdttcub” disminuye “idc”), y entre “avg_totalborn” e “idc” (también negativa, -0,139, pero de menor magnitud)
- Se sospecha que puede existir una relación (0,05 < p < 0,10) entre “cerdttcub” y “fertilidad”(+0,115), y entre “avg_totalborn” y “fertilidad” (+0,122);
- No se puede considerar como estadísticamente significativas el resto de correlaciones (p ≥ 0,10), con lo aceptamos que no hay correlación entre ellas.
Los puntos de los gráficos nos muestran visualmente el sentido de la relación y con los datos de correlación le damos valor. El valor de la p nos indica si la anterior relación es o no estadísticamente significativa, y queda bajo nuestra interpretación técnica el dar más o menos valor a los anteriores datos.
Así, como respuesta a las preguntas que nos hacíamos en un principio:
- Si cubrimos más cerdas en los siete días posteriores al destete, ¿tenemos mayor fertilidad? Sí, pero no de forma muy importante y sólo con una tendencia estadística.
- Si tenemos mayor fertilidad, ¿tenemos más lechones nacidos totales? Sí, pero no de forma muy importante y sólo con una tendencia estadística.
- Si el intervalo destete a celo es menor, ¿tenemos mejor fertilidad? No, la correlación es baja y no estadísticamente diferente de 0.
- Si cubrimos más cerdas en los siete días posteriores al destete, ¿tenemos más lechones nacidos totales? No, la correlación es baja y no estadísticamente diferente de 0.
- Si el intervalo destete a celo es menor, ¿tenemos más nacidos totales? Sí, y es estadísticamente significativo, aunque no de forma muy relevante.
Caso de uso 2: Correlación de tres variables: cerdo, GMD (Ganancia Media Diaria) y CMD (Consumo Medio Diario)
Para obtener el siguiente gráfico, más sencillo esta vez, hemos utilizado una base de datos que incluye tres variables:
- Cerdos: Variable identificador de cada observación
- GMD: Ganancia Media Diaria
- CMD: Consumo Medio Diario
| Cerdo | CMD | GMD |
| 1 | 1.064 | 532 |
| 2 | 1.168 | 556 |
| 3 | 905 | 411 |
| 4 | 1.124 | 562 |
| 5 | 1.100 | 523 |
| 6 | 1.198 | 544 |
| 7 | 935 | 467 |
| 8 | 1.088 | 518 |
| 9 | 1.109 | 554 |
| 10 | 1.009 | 438 |
Siguiendo los pasos explicados en el previo ejemplo, seleccionamos ambas variables y obtenemos el siguiente gráfico:
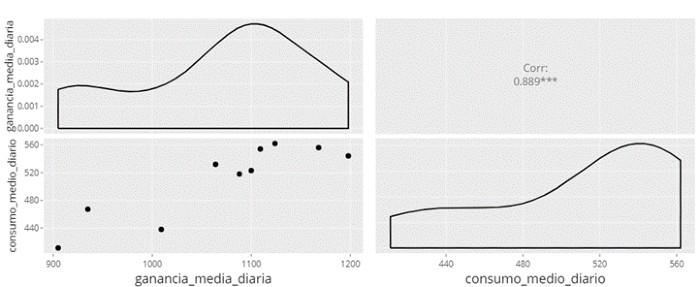
En este caso, el gráfico nos da una idea muy visual de cómo se relacionan las dos variables, así como el valor numérico del estadístico de correlación de ambas variables (0,889) que nos indica que hay una asociación lineal y positiva.
Como conclusión, comentar que el diagrama de dispersión puede estudiar la relación entre[1]:
- Dos factores o causas relacionadas con la calidad.
- Dos problemas de calidad.
- Un problema de calidad y su posible causa.
- Tantas variables como necesitemos para extraer información sobre cómo se comporta nuestro proceso.
[1] Fuente: AEC
Accede a la Web Oficial de Síagro para obtener más información sobre cómo puede tu empresa beneficiarse de una toma de decisiones basada en datos, y por qué acabas de encontrar tu mejor aliado estadístico.