¿Alguna vacuna produce un incremento de temperatura mayor que otras tras seis horas de su aplicación?
Uno de los análisis estadísticos de datos más habitual es aquel en el que se intenta estudiar el efecto que un factor (por ejemplo, un tratamiento) tiene sobre una variable continua (por ejemplo, el peso de los lechones). Para ello, podemos efectuar un test t de Student o un Análisis de la Varianza (comúnmente llamado ANOVA por sus siglas en inglés de de Analysis of Variance).
Mientras que el primero sólo es útil cuando el factor estudiado tiene dos niveles (por ejemplo, el factor tratamiento con los grupos “con probióticos” en el pienso y “sin probióticos”), el ANOVA puede hacerse cuando hay más de dos niveles (por ejemplo, para comparar tres tipos de probióticos).
El ANOVA permite relacionar una variable categórica independiente con una variable cuantitativa continua dependiente a través de la comparación de “c” medias.
El ANOVA explica toda la variación total y cómo esta se distribuye dentro de los grupos, por lo que nos dice si la variabilidad de los grupos es significativamente diferente entre sí.
En este caso, podríamos responder a la pregunta: ¿Parte de la variabilidad en el peso entre lechones se puede explicar por el hecho de que están sometidos a diferentes probióticos? O… ¿tiene el tratamiento algún efecto sobre el peso de los lechones? Todo esto, lo podemos contestar con un ANOVA, donde obtenemos un valor de probabilidad (p value) cuya interpretación es muy sencilla:
- p value < 0,005: Sí existen diferencias significativas entre los grupos.
- p value > 0,05: No existen diferencias significativas entre los grupos.
Por tanto, cuando comparamos nuestro p.value (supongamos que es 2·10-6) con un nivel de significación que es 0,05 (5% de error) podemos aceptar la hipótesis de partida. Siguiendo el ejemplo, un tratamiento afecta a la ganancia media de los lechones. En cambio, si el valor hubiese sido igual o superior a 0,05 (5% de error), debemos aceptar la hipótesis de que el tratamiento no afecta al peso.
En este ejemplo que presentamos a continuación, vamos a explicar todos los números que aparecen en un análisis de varianza (ANOVA), no sólo el p value, que los hemos obtenido con el programa Síagro.
Supongamos que tenemos tres vacunas de una enfermedad cualquiera y que registramos la diferencia de temperatura entre el momento de la aplicación y seis horas tras su aplicación. La pregunta que vamos a contestar es…
¿Alguna vacuna produce un incremento de temperatura mayor que otras tras seis horas de su aplicación?
Para responder esta pregunta hemos utilizado una base de datos que contiene información de dos variables: “Vacuna” (los tres tipos de vacuna) y “Temp” (el incremento de temperatura en ºC desde el momento de la aplicación de la vacuna hasta seis horas después).
- Variable categórica independiente: Vacuna.
- Variable cuantitativa continua dependiente: Temp.
- Comparación de las medias de las tres vacunas: V1, V2 y V3.
| id | vacuna | temp |
| 1 | V1 | 1,48 |
| 2 | V1 | 0,22 |
| 3 | V1 | 1,32 |
| 4 | V1 | 0,96 |
| 5 | V1 | 1,1 |
| 6 | V2 | 0,5 |
| 7 | V2 | 1,6 |
| 8 | V2 | 0,24 |
| 9 | V2 | 1,56 |
| 10 | V2 | 0,56 |
| 11 | V3 | 1,46 |
| 12 | V3 | 0,46 |
| 13 | V3 | 0,76 |
| 14 | V3 | 0,8 |
| 15 | V3 | 1,16 |
Como siempre, debemos apoyarnos en la hipótesis nula (Ho) que se quiere comprobar, en este caso, “no hay diferencias entre los incrementos de temperatura entre las vacunas”.
Pero no se empieza una casa por el tejado. Previo a un análisis ANOVA, debemos explorar nuestros datos:
- Buscar anomalías o valores extraños,
- comprobar la normalidad de la variable respuesta dentro de cada grupo (de cada vacuna), y
- comprobar la homogeneidad de las varianzas (homocedasticidad) y que los valores sean independientes.
Esto es debido a que los cálculos del ANOVA se basan en el cumplimiento de estas tres premisas y, si realizamos este análisis cuando estas no son ciertas, es muy probable que lleguemos a conclusiones erróneas.
Afortunadamente, todos estos cálculos los hace Síagro de manera automática dentro de Modelos de Predicción/ANOVA. Simplemente seleccionamos nuestras variables y obtenemos los resultados:
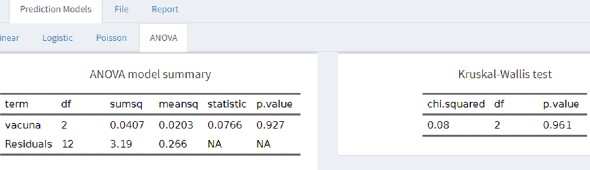
- df: grados de libertad.
- Sumsq: Suma de cuadrados.
- Meansq: Media de cuadrados.
- statistic: valor de F.
- p value: valor de probabilidad de F
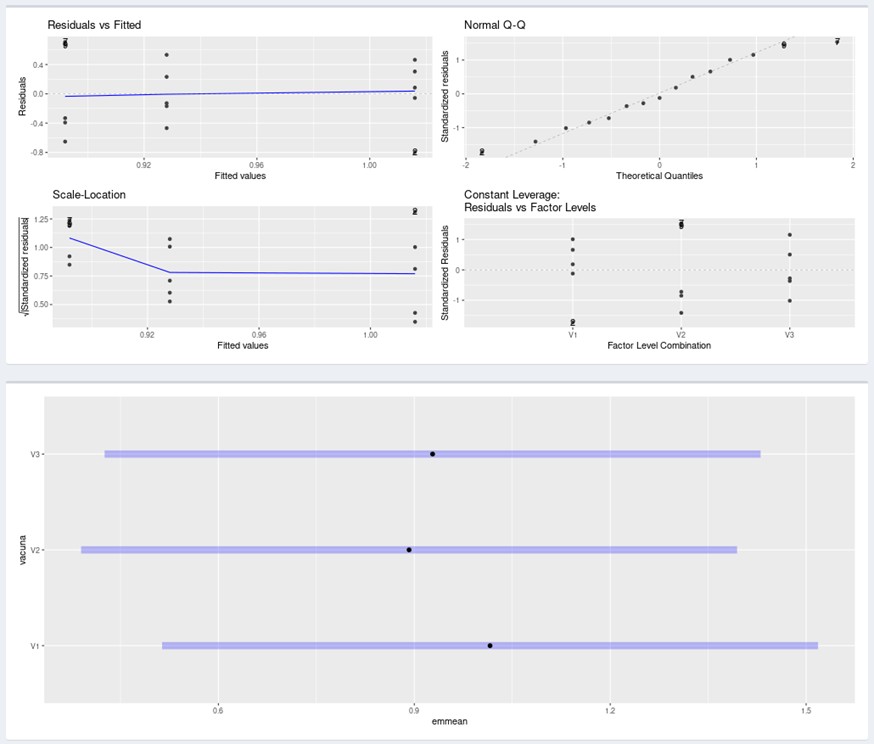
En realidad, podemos también hacer la comprobación de estos supuestos dentro del Análisis Exploratorio de Síagro si nos sentimos más cómodos:
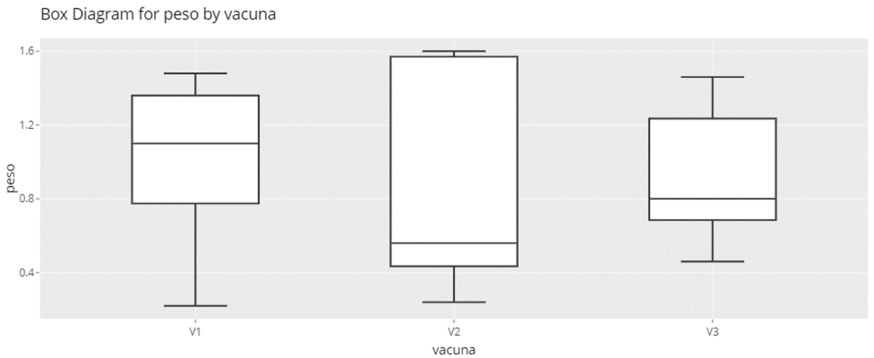
Primero, realizamos un boxplot de las temperaturas por grupos y seleccionamos ambas variables en el panel de control. Obtendremos el mismo gráfico de cajas donde vemos que no existe ningún dato anómalo (outlier) y que el incremento de la temperatura parece a simple vista diferente entre las vacunas, y el resumen de los datos:
Interpretación: Como nuestro p value es 0,927 (mayor a 0,05) podemos decir con evidencia que no existen diferencias estadísticamente significativas entre los tres grupos y la vacuna no ha afectado a la temperatura de los lechones seis horas después de su aplicación.
Resumen por peso
| Min | Mean | Median | Max | Variance |
|---|---|---|---|---|
| 0,22 | 0,945 | 0,96 | 1,6 | 0,231 |
Resumen por vacuna
| vacuna | Min | Mean | Median | Max | Variance |
|---|---|---|---|---|---|
| V1 | 0,22 | 1,02 | 1,1 | 1,48 | 0,238 |
| V2 | 0,24 | 0,892 | 0,56 | 1,6 | 0,409 |
| V3 | 0,46 | 0,928 | 0,8 | 1,46 | 0,15 |
En segundo lugar, para comprobar la normalidad se pueden utilizar todos los datos sin diferenciar por vacunas, pero más correcto es hacerlo separando por grupos, algo que Síagro nos permite hacer en el Test de Normalidad (o Normality Test).
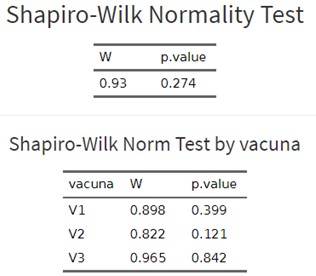
Se observa que ni en su conjunto ni en ninguno de los tres grupos por individual se vulnera (p value es mayor a 0,05).
Para la tercera premisa, la comprobación de la homogeneidad de varianzas, se puede hacer dentro del análisis ANOVA.
Para complementar el análisis, en Análisis Exploratorio/Balance también habremos obtenido los siguientes datos (medias y desviaciones típicas de cada grupo) que nos ayudan a entender cómo se comporta la variabilidad en términos de desviación típica dentro de cada grupo:
| V1 (N=5) Mean | V1 (N=5) Std.Dev | V2 (N=5) Mean | V2 (N=5) Std. Dev. | V3 (N=5) Mean | V3 (N=5) Std. Dev. | |
|---|---|---|---|---|---|---|
| temp | 1,0 | 0,5 | 0,9 | 0,6 | 0,9 | 0,4 |
Síagro incluye muchos más modelos estadísticos para analizar datos
Este es solo un ejemplo de todo lo que el programa es capaz de analizar, por lo que invitamos a todos los lectores a visitar la página web oficial haciendo clic aquí y descubrir el mundo Síagro.