Análisis de series temporales III:

abortos otoñales

Artículo nº125 de Suis.

En los dos números anteriores hemos introducido las series temporales (ver 123 y 124). Para recordar diremos que una serie temporal es una secuencia de datos medidos en determinados momentos y ordenados cronológicamente. Su análisis nos interesa especialmente porque podemos describir o explicar qué ha sucedido con esa variable en el pasado y también porque queremos predecir cómo se comportará probablemente en el futuro.
Para recordar cómo podíamos describir matemáticamente una serie de datos diremos que cada dato de dicha serie es la suma (modelo aditivo) de varias componentes:

Xt = Tt + St + It o

Valor observado = Tendencia + Estacionalidad + Irregular

Estudiamos también si nuestros datos tenían una tendencia estacional y lo hicimos con R. Volvemos a cargar los datos con los que estuvimos trabajando (puedes descargar el archivo «abortionmes.csv» haciendo clic aquí) y para ello, iniciaremos R y cargaremos ante todo el paquete “timeSeries” que nos permitirá realizar los análisis que queremos. Para ello iremos a la consola de R (donde cargamos habitualmente RCommander) e iniciaremos el paquete “timeSeries” y “RCommander” escribiendo estas dos instrucciones:

library (timeSeries)
library (Rcmdr)

Una vez instalado, cargaremos el archivo «abortionmes.csv». A estos datos les llamaremos “abortionsmes” igual que en el número anterior. Verificaremos que los datos están cargados viendo que en RCommander, en la esquina superior izquierda, aparece la etiqueta “abortionsmes”.

Lo último que hicimos y sobre lo que incidimos de nuevo es en la descomposición de nuestros datos en tres componentes: la tendencia, la estacionalidad y la componente aleatoria. Para ello escribimos en la pantalla de instrucciones de RCommander:

abort.ts <- ts(abortionmes, frequency=12, start=c(2012,1))

Donde le decimos a R que nuestros datos “abortionsmes” son mensuales (frequency=12) y que comienzan en el año 2012, correspondiendo el primer dato a enero de 2012 [start=c(2012, 1)].

A continuación, escribiremos en la pantalla de comandos de RCommander la siguiente instrucción:

abort.sc <- decompose(abort.ts)

Si ahora escribimos:

abort.sc$seasonal

R nos devolverá el grupo de datos de la siguiente tabla:

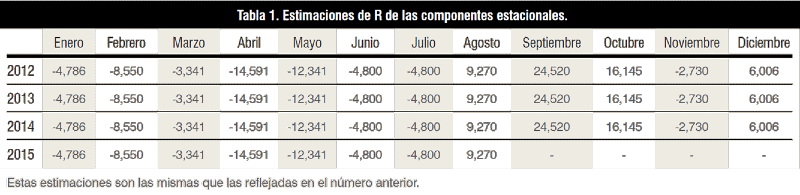
Únicamente se ha cambiado la nomenclatura. En el número anterior lo llamábamos:

“abortimeseriescomponents”; ahora “abort.sc”.

Podemos ver que el mayor factor estacional se da para los meses de septiembre y octubre de cada año.  Si escribimos:

plot(abort.sc)

Lo que vamos a hacer ahora es quitar la estacionalidad a esta serie temporal.

¿Por qué?

Hemos oído y visto mucho este término en datos que ofrece el gobierno cuando habla del empleo o cuando se dan cifras macroeconómicas que tienen una periodicidad. Por ejemplo, los datos desestacionalizados del paro son los datos corregidos teniendo en cuenta que hay diferencias sistemáticas en las series de datos según el momento concreto del año. Los no desestacionalizados no llevan el ajuste correspondiente.

Siguiendo con este ejemplo, para saber si una medida del gobierno introducida en mayo tiene efecto sobre los niveles de paro, hay que eliminar el efecto estacional del verano para saber si es efectiva o no. Con nuestros datos sucederá lo mismo.

¿Cómo? R nos ayuda

Restamos la componente estacional de los datos originales. Para ello ejecutaremos la siguiente instrucción en R:

abort.adj <- abort.ts – abort.sc$seasonal

Y tendremos los datos desestacionalizados. Lo podemos comprobar con un simple cálculo. Si tomamos el valor original de los abortos en el mes de enero de 2012 (12) y le restamos el valor del mes de enero del 2012 dado en la tabla 1 (-4,785880) el resultado es 16,785880.
Ahora podemos hacer un gráfico de los datos desestacionalizados con:

plot(abort.adj)

Y si además usamos la siguiente instrucción, veremos el gráfico con los datos originales y el gráfico con los datos desestacionalizados (figura 1):

par(mfrow=c(1,2))plot(abort.ts)plot(abort.adj)

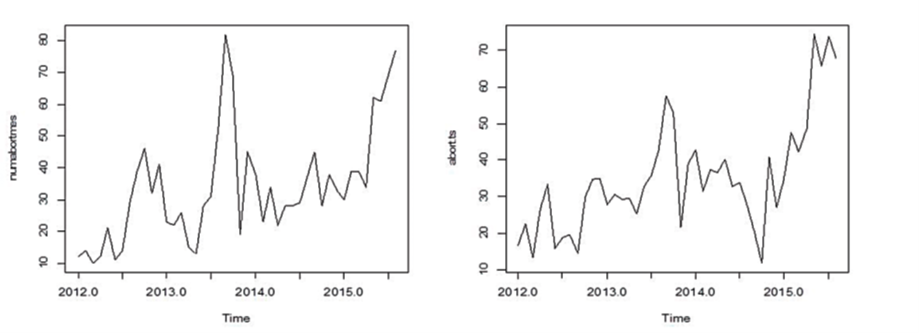
Ahora los datos sólo contienen la componente de tendencia y la irregular.

En este apartado retrocedemos un poco, ya que iniciamos estos números dedicados a las series temporales y rápidamente comenzamos a trabajar con los datos de los abortos de una granja. No vimos nada acerca de cómo eran los datos y ahora que ya sabemos hacer análisis de una serie temporal introduciremos algunos conceptos necesarios. Por ejemplo, las series temporales pueden ser estacionarias o no estacionarias. ¿Cómo sabemos si tenemos una serie temporal estacionaria?

Una serie es estacionaria cuando es estable a lo largo del tiempo. Dicho matemáticamente, cuando su media y varianza son constantes en el tiempo. Esto se refleja gráficamente en que los valores de la serie tienden a oscilar alrededor de una media constante y la variabilidad con respecto a esa media también permanece constante en el tiempo.

Por el contrario, una serie temporal es no estacionaria si la tendencia y/o la variabilidad cambian en el tiempo. Los cambios en la media determinan una tendencia a crecer o decrecer a largo plazo, por lo que la serie no oscila alrededor de un valor constante.

Evidentemente, nuestra serie original no era estacionaria y para analizarla y hacer predicciones, necesitamos que lo sea. Una de las formas más fáciles de transformar una serie no estacionaria en estacionaria es crear una nueva serie de valores de tal forma que los nuevos valores serán la diferencia del siguiente con el actual. Por ejemplo, si el dato de los abortos del mes de enero de 2012 era 12 y el de febrero 14, nuestro primer valor nuevo será 2. Y así sucesivamente. En R esto es muy fácil de realizar:

abort.ts.diff1 <- diff(abort.ts, differences=1)

Y nos genera una serie nueva de valores que si los ponemos en un gráfico mediante:

plot (abort.ts.diff1)

obtenemos el siguiente gráfico.

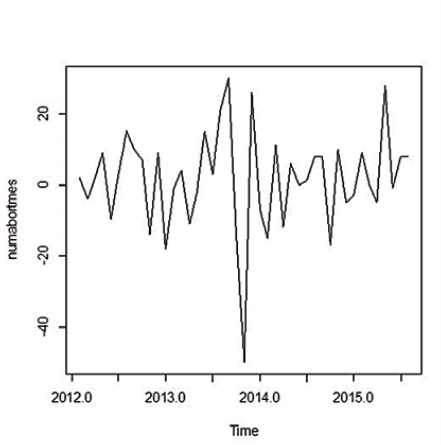
Datos diferenciados en una unidad de los abortos de una granja.

Como vemos es muy diferente al gráfico de nuestros datos originales.

En el próximo número veremos la utilidad de esta herramienta y realizaremos predicciones creando un modelo matemático al efecto.