Análisis de series temporales IV:

abortos otoñales

Artículo nº126 de Suis

En los tres números anteriores hemos introducido las series temporales (ver 123, 124 y 125). Para recordar diremos que una serie temporal es una secuencia de datos medidos en determinados momentos y ordenados cronológicamente. Nos interesa especialmente su análisis porque podemos describir o explicar qué ha sucedido con esa variable en el pasado y también por qué queremos predecir cómo se comportará en el futuro.
Para recordar cómo podíamos matemáticamente describir una serie temporal vimos que una serie temporal de datos es la suma (modelo aditivo) de varias componentes que podemos presentar como:

Valor observado = Tendencia + Estacionalidad + Irregular

Donde la tendencia es el comportamiento de la serie a largo plazo, la estacionalidad son los movimientos de oscilación dentro de un año y la irregularidad, o valor aleatorio, son los movimientos oscilatorios de la serie alrededor de los componentes anteriores no controlados por el modelo.

Volvemos a cargar los datos con los que estuvimos trabajando y para ello, iniciaremos R y cargaremos antes el paquete “timeSeries” que nos permitirá realizar los análisis que queremos. Para ello iremos a la consola de R (donde cargamos habitualmente RCommander) e iniciaremos los paquetes “timeSeries” y “RCommander” escribiendo estas dos instrucciones:

library (timeSeries)
library (Rcmdr)

Una vez instaladas, cargaremos el archivo “abortionsmes.csv”.
A estos datos les llamaremos “abortionsmes”, igual que en los números anteriores. Verificaremos que los datos están cargados viendo que en RCommander, en la esquina superior izquierda, aparece la etiqueta “abortionsmes”.

En los números anteriores vimos cómo descomponer nuestros datos en tres componentes: la tendencia, la estacionalidad y la componente aleatoria.
Primero convertiremos nuestros datos en una serie temporal mediante la instrucción (que escribimos en la pantalla de instrucciones de RCommander):

abort.ts <- ts(abortionmes, frequency=12, start=c(2012,1))

Donde le decimos a R que nuestros datos “abortionsmes” son mensuales (frequency=12) y que comienzan en el año 2012, correspondiendo el primer dato a enero de 2012 [start=c(2012, 1)].

Los componentes de las series temporales

Para descomponer la serie de datos temporales, escribiremos en la pantalla de comandos de RCommander la siguiente instrucción:

abort.sc <- decompose(abort.ts)

Podemos ver que el mayor factor estacional se da para los meses de septiembre y octubre de cada año:

plot(abort.sc)

Para desestacionalizar los datos de nuestra serie lo que hicimos fue restar la componente estacional de los datos originales. Para ello ejecutaremos la siguiente instrucción en R:

abort.adj <- abort.ts – abort.sc$seasonal

Y tendremos los datos desestacionalizados. Ahora podemos hacer un gráfico de los datos desestacionalizados y de los datos originales (ver siguiente gráfico):

par(mfrow=c(1,2))

plot(abort.ts)

plot(abort.adj)

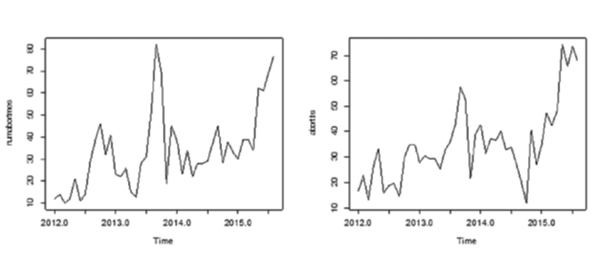
Datos originales y desestacionalizados de los abortos de una granja.

Para terminar esta serie de artículos sobre series temporales vamos a introducir cómo construir un modelo matemático que nos permita predecir futuros valores o modelizar los que tenemos. Nuestra serie tiene estacionalidad y, además, tiene una tendencia al alza con el tiempo. Esto es interesante ya que el modelo que deberemos usar depende de estos factores.

Para modelizar esta serie, debemos primero tener instalado el paquete “forecast”. Para ello, iremos a la pantalla principal de R y en Paquetes/Instalar paquete(s)…, elegiremos una localización para la descarga, por ejemplo Spain (Madrid) y posteriormente elegiremos el paquete “forecast” de la lista. Una vez descargado, lo cargaremos en R mediante la instrucción: library(forecast)

Y ya podremos comenzar a usar este paquete.

Función Holt-Winters

Vamos a usar una función denominada Holt-Winters. Es una función que modeliza mediante un algoritmo exponencial suavizado, teniendo en cuenta que nuestros datos tienen tendencia y estacionalidad. Esta función estima el nivel, la pendiente y la estacionalidad de los datos en un determinado momento del tiempo.

El suavizado está controlado por tres parámetros: alfa, beta y gamma para las estimaciones del nivel, de la pendiente b del componente de la tendencia y de la componente estacional, respectivamente, en un momento del tiempo. Estos tres parámetros (alfa, beta y gamma) oscilan entre 0 y 1, de forma que un valor cercano a 0 significa que el valor de las últimas observaciones tiene poco peso específico en la predicción o modelización.

Para hacer predicciones con nuestros datos primero transformamos la serie temporal original en su logaritmo (para tener una mejor linealidad y predicción) con la instrucción log(abortionmes.ts). Luego, usaremos la función HoltWinters(), para poder hacer predicciones. Si escribimos en la pantalla de instrucciones de RCommander:

logabortionmes<-log(abortionmes.ts)

Transformamos los datos. Luego con:

abortionmes.forecast<-HoltWinters(logabortionmes)

Aplicamos la función HoltWinters() a los datos transformados y con:

abortionmes.forecast

Estimamos los parámetros alfa, beta y gamma. Esta es la salida que nos da RCommander:

> abortionmes.forecastHolt-Winters exponential smoothing with trend and additive seasonal component.

Call:
HoltWinters(x = logabortionmes)
Smoothing parameters: 
alpha: 0.4491101 
beta : 0 
gamma: 0.5925443

El valor alfa = 0,45 es relativamente bajo indicando que la estimación del nivel en cada momento está basada en las observaciones recientes y en algunas observaciones más distantes en el tiempo.

El valor beta = 0, indica que la estimación de la pendiente de la componente de la tendencia no cambia con el tiempo.

Contrariamente, el valor de gamma = 0,59 es moderadamente alto indicando que la componente estacional en cada momento está basada en las observaciones más recientes.

Gráficos

Podemos ver un gráfico de los valores originales y los estimados con esta función mediante:

plot(abortionmes.forecast)

Obteniendo el gráfico que se observa a continuación:

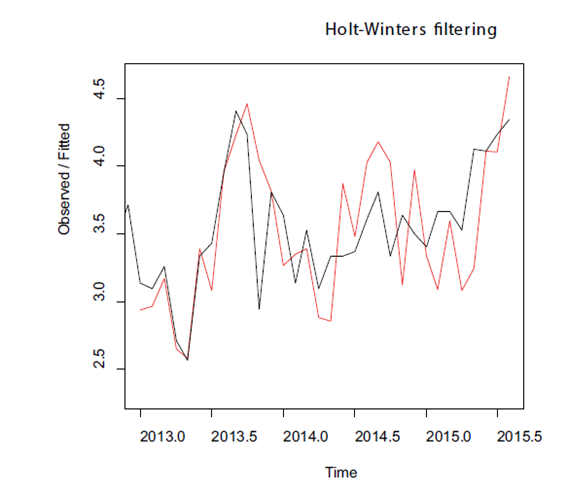
Valores transformados y predichos de los abortos de una granja de cerdas (datos en logaritmos).

Podemos ver que las predicciones de incrementos de abortos en el otoño son bastante acertadas con esta función.

Para hacer predicciones futuras no incluidas en la serie original de datos, usaremos la función “forecast.HoltWinters()”. Nuestros datos originales eran desde enero de 2012 hasta agosto de 2015.

Si queremos predecir los abortos entre septiembre de 2015 y marzo de 2016 (7 meses) y ver una gráfica, podemos escribir:

abortionmes.forecast2<-forecast.HoltWinters(abortionmes.forecast, h=7)
plot.forecast(abortionmes.forecast2)

Y obtendremos el siguiente gráfico:

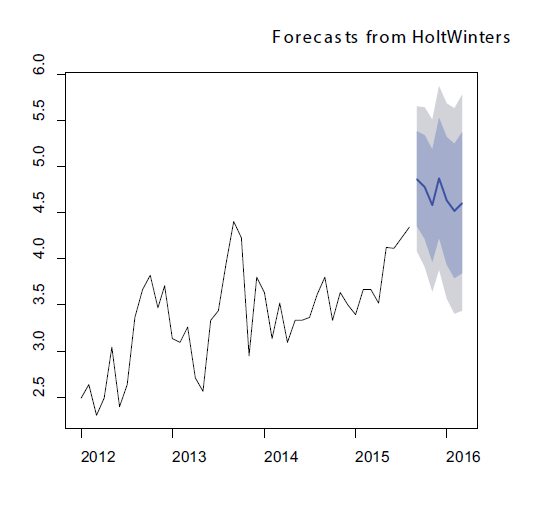
Predicciones de los abortos en una granja de cerdas (datos en logaritmos de los valores originales).

Los valores predichos están en la línea azul y las bandas gris oscura y gris clara son los valores de los intervalos de confianza 80 % y 95 % respectivamente, con lo que tenemos un método que nos permite predecir qué va a ocurrir en nuestra granja con diferentes parámetros.