Minería de datos (V): Análisis de componentes principales
¿Demasiada información para comprender qué es lo que pasa? La técnica del análisis de componentes principales nos ayuda.
Es habitual que al recoger información de la producción porcina en cualquiera de sus etapas (reproductoras, lechones tras su destete o cerdos en engorde) tengamos muchísimas variables.
Imaginemos que queremos comprender qué es lo que pasa en nuestro sistema o queremos encontrar patrones de comportamiento entre las diferentes variables. Una técnica que podríamos usar sería ver las correlaciones que existen entre las diferentes variables.
Por ejemplo: a mayor mortalidad, ¿tengo mayor coste de medicinas? Otro ejemplo podría ser si el coste por tonelada del alimento nos da un mejor crecimiento diario. Esto lo podríamos realizar con un análisis de correlación y con un gráfico. La correlación está íntimamente ligada con la regresión en el sentido de que se centra en el estudio del grado de asociación entre variables. Por lo tanto, una variable independiente que presente un alto grado de correlación con una variable dependiente será muy útil para predecir los valores de ésta última. Cuando la relación entre las variables es lineal se habla de correlación lineal. Una de las medidas más utilizadas para medir la correlación lineal entre variables es el coeficiente de correlación lineal de Pearson1.
Hagámoslo. Yendo a nuestro blog buscaremos el fichero que se llama “pca.csv”. Una vez escargado el fichero, iremos a R, cargaremos el paquete “RCommander” mediante la instrucción library(Rcmdr). Una vez cargado RCommander importaremos el archivo “pca.csv” yendo a “Datos/Importar conjunto de datos/Desde un archivo de texto, portapapeles o URL” y lo denominaremos, “pca”. Si hacemos un resumen de los datos yendo a estadísticos/Resúmenes/Conjunto de datos activos obtendremos los resultados de la figura 1.
Este es un conjunto de datos creado para esta ocasión. Como se puede ver no existen datos faltantes (NA) en ninguna variable. Podemos ver que los nombres de las variables son bastante explícitos para el lector de producción porcina.
Imaginemos que para estudiar la eficacia de un aditivo en el pienso en vez de realizar el típico estudio con una serie de corrales en una granja con el pienso control y otros con el pienso experimental, hemos entrado 300 lotes de cerdos en los sitios 2 durante un año que provienen de una serie de granjas de cerdas. Aleatorizamos cada lote que entraba en un destete, le asignábamos o no el producto experimental en el pienso y en cada sitio 2 replicábamos el estudio 4 veces que podían o no ser consecutivas.
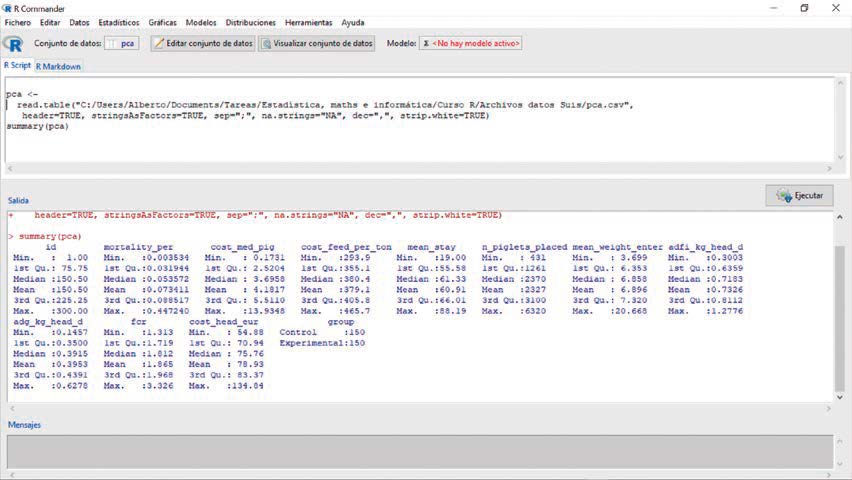
Figura 1: Resúmenes numéricos del conjunto de datos “pca”.
Hemos extraído una serie de variables al finalizar el estudio y queremos ver si existen patrones en nuestros datos ya que queremos ver la eficacia del aditivo en todo nuestro sistema.
Comenzamos a explorar la relación entre variables para entender nuestro conjunto de datos. ¿Existe relación entre el consumo diario y la ganancia diaria? Para estudiar si estas variables están correlacionadas entre ellas vamos a “Estadísticos/Resúmenes/Matriz de correlaciones” y elegimos las variables “adfi_kg_head_d” y “adg_kg_head_d”. Elegimos que las observaciones a usar sean “Parejas de casos completos”, marcamos la casilla de “p-valores pareados” y obtendremos el siguiente resultado:
> rcorr.adjust(pca[,c(“adfi_kg_head_d”,”adg_
kg_head_d”)], type=”pearson”, use=”pairwise.
complete”)
Pearson correlations:
adfi_kg_head_d adg_kg_head_d
adfi_kg_head_d 1.0000 0.7848
adg_kg_head_d 0.7848 1.0000
Number of observations: 300
Pairwise two-sided p-values:
adfi_kg_head_d adg_kg_head_d
adfi_kg_head_d <.0001
adg_kg_head_d <.0001
Adjusted p-values (Holm’s method)
adfi_kg_head_d adg_kg_head_d
adfi_kg_head_d <.0001
adg_kg_head_d <.0001
Podemos deducir, que efectivamente ambas variables están correlaciones significativamente. Lo podemos ver en un gráfico yendo a “Gráficas/Diagrama de dispersión…”, eligiendo la variable “adfi_kg_head_d” en el eje x, “adg_kg_head_d” en el eje y, y en “Opciones” marcando la casilla “Líneas de mínimos cuadrados”. Obtendremos la figura 2.
Sin embargo, nuestro conjunto de datos tiene 10 variables cuantitativas (hay 2 variables que no lo son: el identificador de lote, “id” y el grupo, “group”), por lo que si generamos las correlaciones dos a dos, existen 45 posibles coeficientes de correlación, lo que hace difícil su comprensión.
Otro problema que tenemos cuando estudiamos conjuntos de datos muy grandes o con muchas variables de producción es la fuerte correlación que muchas veces se presenta entre variables: si tomamos demasiadas variables (lo habitual cuando desconocemos qué vamos a estudiar, qué va a pasar o si solo queremos estudiar los datos) lo normal es que estén relacionadas entre sí o midan cosas parecidas, pero desde puntos de vista diferentes. Por ejemplo, una baja mortalidad suele traer conjuntamente un buen índice de conversión.
Por lo tanto, se hace necesario reducir el número de variables. No obstante, es importante señalar el hecho de que el concepto de más información se relaciona con el de mayor variabilidad. Cuanto mayor sea la variabilidad de los datos (varianza) más información se considera que existe.
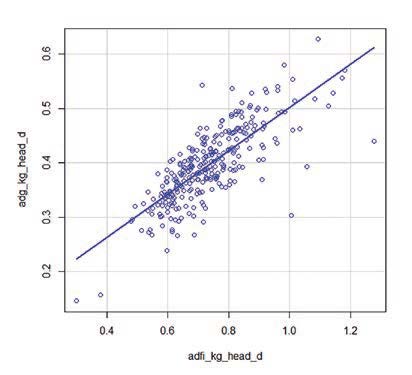 Figura 2: Gráfico de dispersión entre las variables.
Figura 2: Gráfico de dispersión entre las variables.
Pero para ello Pearson a finales del siglo XIX y Hotelling en los años 30 del siglo XX desarrollaron unas técnicas que se han denominado análisis de componentes principales (Principal Component Analysis, PCA en inglés) que nos ayudan a estudiar las relaciones que se presentan entre un conjunto p de variables correlacionadas transformando el conjunto original de variables en otro nuevo conjunto de variables no correlacionadas (m variables) entre sí que se denomina conjunto de componentes principales y que reduce el número de variables de tal forma que el nuevo conjunto de datos captura la mayor parte de la información sin información redundante.
Las nuevas variables son combinaciones lineales2 de las anteriores y se van construyendo según el orden de importancia en cuanto a la variabilidad total que recogen de la muestra.
De modo ideal, se buscan m<p variables que sean combinaciones lineales de las p originales y que no estén correlacionadas, recogiendo la mayor parte de la información o variabilidad de los datos. Si las variables originales no están correlacionadas no tiene sentido realizar un análisis de componentes principales. En ese caso el número de componentes principales sería igual al de variables iniciales con lo que el análisis no aportaría nada.
El análisis de componentes principales es una técnica matemática de síntesis que no requiere la suposición de normalidad multivariante de los datos, aunque si esto último se cumple se puede dar una interpretación más profunda de dichos componentes. Evidentemente no es objetivo de estos artículos el mostrar todo el desarrollo matemático que subyace en esta técnica estadística. Pero a medida que vayamos realizando el estudio iremos dando unas sencillas explicaciones de cómo se obtienen los resultados de un PCA y qué significan3.
Cuanto mayor sea la variabilidad de los datos (varianza) más información se considera que existe.
Lo primero que vamos a realizar es crear un nuevo conjunto a partir de nuestros datos pca. Eliminaremos las variables “id” y “group” aunque con posterioridad, en siguientes artículos las usaremos. Para crear el nuevo conjunto que denominaremos pca2, escribiremos en la pantalla:
pca2 <- within(pca, { group <- NULL id <- NULL })
Comenzaremos aplicando a nuestro nuevo conjunto de datos pca2 la función de R que ejecuta un análisis de componentes principales, prcomp(), escribiendo en la pantalla:
res_pca <- prcomp(pca2, scale = TRUE)La función prcomp() nos devolverá tres resultados. El primero denominado X, contiene las componentes principales para dibujar un gráfico que usaremos a continuación. Como tenemos 10 variables tendremos 10 componentes principales. Explicaremos esto en el siguiente artículo. De momento basta con saber que cada variable ha sido escalada (por eso en la función prcomp() el argumento scale está fijado en TRUE). Esto se realiza porque las diferentes variables tienen diferentes unidades de medida y sería difícil compararlas entre sí.
La primera componente principal explicará la mayor proporción de variabilidad de los datos originales y así sucesivamente. Para obtener un gráfico de PCA usamos las dos primeras componentes principales (PC1 y PC2) aunque a veces podemos usar la tercera y cuarta (PC3 y PC4).
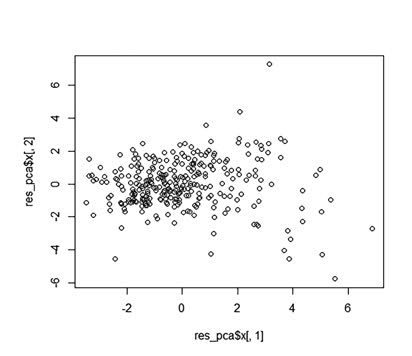
Para obtener el gráfico con las dos primeras componentes, escribiremos:
plot(res_pca$x[,1], res_pca$x[,2])¿Cuánta variabilidad representa la primera componente principal (pc1) denominada en el gráfico como res_pca$x[,1]? Usaremos el cuadrado de la desviación estándar para calcular cuánta variación de los datos originales representa pc1. Y como es más fácil verlo en porcentajes, lo calcularemos. En la consola escribiremos:
pca-var <- res_pca$sdev^2 pva.var.per <- round(pca.var/sum(pca. var)*100, 1)
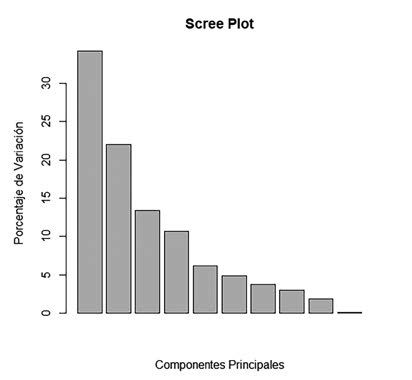
y creando un gráfico con estos porcentajes es más fácil de interpretarlo. Un gráfico de barras nos servirá.
barplot(pca.var.per, main = “Scree Plot”, xlab = “Componentes Principales”, ylab = “Porcentaje de Variación”)
Entre las componentes principales 1 a 4 tenemos explicado el 80,3% de la variabilidad total. Las variables “cost_head_eur”, “cost_feed_per_ton”, “cost_med_
pig” y “fcr” son las variables que más variabilidad aportan al conjunto de nuestros datos. ¿Cómo hemos sabido esta información? En el siguiente artículo veremos cómo obtener esta información y usaremos un paquete creado para realizar análisis de componentes principales muy útil que hace que realizar un PCA sea muy sencillo: FactoMineR.
REFEFENCIAS
1. Análisis de componentes principales – Yasmin Sánchez
2. Una combinación lineal puede mostrarse como y = a + bx, siendo x la variable explicativa e y la variable explicada. a y b son coeficientes.
3. StatQuest with Josh Starmer en YouTube es una fantástica herramienta para comprender de forma fácil qué hace y cómo lo hace un PCA.
AUTORES
Alberto Morillo Alujas – Tests and Trials SLU
Daniel Villalba Mata2 – Universidad de Lleida
Óscar Salinas Pérez – Tests and Trials SLU
Emilio López Cano – Universidad Rey Juan Carlos (Madrid)