Medidas repetidas de sujetos
En el número anterior comenzamos a estudiar y a analizar registros de individuos que dentro de una investigación tenían variables o características que se repetían en el tiempo o que cambiaban de un estado inicial a otro final. Por ejemplo, la temperatura antes y después de un tratamiento. Veíamos que en el fichero de datos denominado “pareados” había diferentes individuos que tenían temperaturas registradas en dos tiempos, T_1 y T_2. Además, vimos que esos mismos datos podíamos verlos en dos formatos, “wide” y “long” como mostramos a continuación.
Tabla 1: Datos pareados en formato «long»
| Id | Temperatura | Tiempo |
|---|---|---|
| 1 | 37,97 | T_1 |
| 2 | 37,37 | T_1 |
| 3 | 37,26 | T_1 |
| 4 | 37,73 | T_1 |
| 5 | 37,41 | T_1 |
| 6 | 37,10 | T_1 |
| 7 | 37,75 | T_1 |
| 8 | 37,55 | T_1 |
| 9 | 37,37 | T_1 |
| . | ||
| 1 | 37,07 | T_2 |
| 2 | 37,03 | T_2 |
| 3 | 37,46 | T_2 |
| 4 | 37,93 | T_2 |
| 5 | 37,37 | T_2 |
| 6 | 37,81 | T_2 |
| 7 | 37,48 | T_2 |
| 8 | 37,96 | T_2 |
| 9 | 37,24 | T_2 |
Tabla 2: Datos pareados en formato «wide»
| Id | T_1 | T_2 |
|---|---|---|
| 1 | 37,97 | 37,07 |
| 2 | 37,37 | 37,03 |
| 3 | 37,26 | 37,46 |
| 4 | 37,73 | 37,93 |
| 5 | 37,41 | 37,37 |
| 6 | 37,10 | 37,81 |
| 7 | 37,75 | 37,48 |
| 8 | 37,55 | 37,96 |
| 9 | 37,37 | 37,24 |
Por otro lado, vimos que usábamos un test t-Student (comprobando antes la normalidad de los datos y cómo eran sus varianzas) para analizar datos pareados y comprobábamos la normalidad en cada uno de los tiempos.
En el estudio de datos pareados se demuestra que lo correcto es realizar la prueba de normalidad a partir de las diferencias d, entre los valores bajo las dos condiciones que representa la variable dependiente[1]. Así, lo primero que debemos hacer para un correcto estudio, es calcular la diferencia entre los valores de las temperaturas T_1 y T_2.
Si cargamos de nuevo los datos de nuestro fichero problema, podemos obtener esta nueva variable de una forma muy fácil. Escribiendo en la pantalla la siguiente instrucción generaremos esa variable que denominaremos d que será la diferencia entre T_2 y T_1:
pareados$d <-pareados$T_2 - pareados$T_1
y lo podemos comprobar, escribiendo:
pareados
y obtendremos:
> pareados id T_1 T_2 d 1 1 37.97 37.07 -0.90 2 2 37.37 37.03 -0.34 3 3 37.26 37.46 0.20 … 38 38 37.96 37.51 -0.45 39 39 37.66 37.27 -0.39 40 40 37.46 37.55 0.09
Ahora…
…ya podemos comprobar correctamente la normalidad de nuestro conjunto de datos y también podríamos hacer un boxplot para ver cómo se distribuyen esas diferencias. Pero antes, para que RCommander entienda que tiene una nueva variable en el conjunto de datos “pareados”, debemos ir a Datos/Conjunto de datos activos/Actualizar conjunto de datos activo.
Para ver un boxplot, iremos a Gráficas/Diagrama de caja y elegir la nueva variable d. En Opciones podemos poner títulos y cambiar colores y veremos que nuestra variable tiene esta forma:
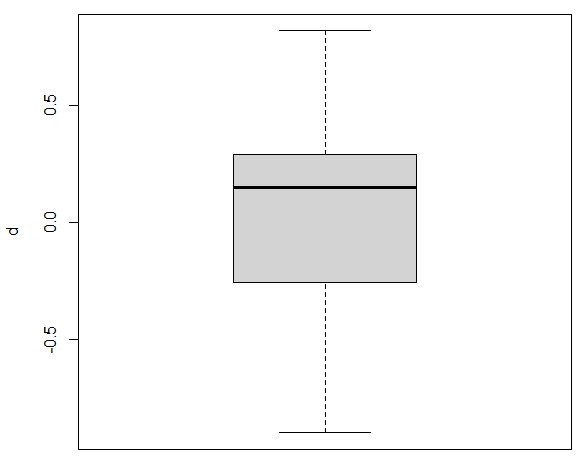
Figura 1: Boxplot de la variable d (descargar gráfico)
Comprobemos la normalidad
Para comprobar la normalidad iremos a Estadísticos/Resúmenes/Test de normalidad, elegiremos la nueva variable d y obtendremos:
> normalityTest(~d, test="shapiro.test", data=pareados)
Shapiro-Wilk normality testdata: d
W = 0.95868, p-value = 0.151
que a diferencia de nuestro número anterior no presenta ninguna anormalidad.
Si ahora vamos a realizar un test t-Student, al tener la nueva variable d que es la diferencia entre T_2 y T_1, ya no necesitamos hacer un test de muestras relacionadas. Podríamos obtener los mismos resultados realizando un test t-Student para una muestra.
Vamos a comprobarlo.
Primero recordaremos el ejercicio del número anterior. Yendo a Estadísticos/Medias/Test t para datos relacionados y elegimos en la primera variable T_2 y en la segunda T_1, obtendremos:
> with(pareados, (t.test(T_2, T_1, alternative='two.sided', conf.level=.95, paired=TRUE))) Paired t-test data: T_2 and T_1 t = 0.61871, df = 39, p-value = 0.5397 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.09417183 0.17717183 sample estimates: mean of the differences 0.0415
Si ahora vamos a Estadísticos/Medias/Test t para una muestra y ahora elegimos la variable d, obtendremos:
with(pareados, (t.test(d, alternative='two.sided', mu=0.0, conf.level=.95)))
One Sample t-test data: d t = 0.61871, df = 39, p-value = 0.5397 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: -0.09417183 0.17717183 sample estimates: mean of x 0.0415
Y como el lector podrá comprobar, obtenemos exactamente el mismo resultado.
¿Cuáles son las conclusiones?
Cuando el cambio del tratamiento no modifica la respuesta, en nuestro caso la variable d, la diferencia es cero. Y si observamos ambas salidas, cuando nos informa sobre el intervalo de confianza 95% de la diferencia (95 percent confidence interval), el intervalo que nos muestra incluye el valor “0”. Si el cambio de T_1 a T_2 modificase la respuesta la diferencia media sería diferente de cero.
Un ejercicio muy ilustrativo es hacer un gráfico de dispersión entre las variables T_1 y T_2. Si vamos a Gráficas/Gráfico de dispersión y elegimos para el eje x, la variable T_1 y para el eje y la variable T_2, obtendremos el siguiente gráfico:
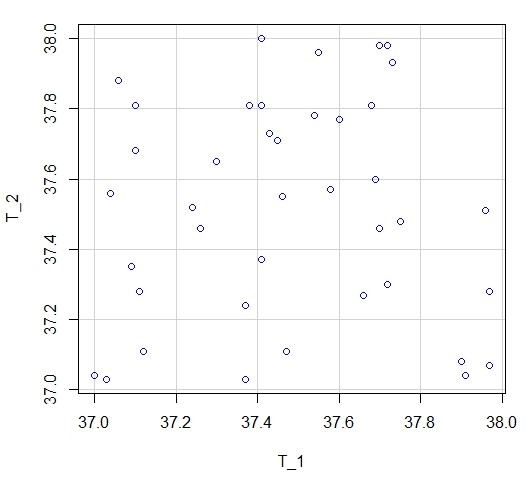
Figura 2: Gráfico de dispersión entre las variables T_1 y T_2 (descargar gráfico)
¿Están relacionadas las variables?
¡Por supuesto que no! Si lo hubieran estado los puntos estaría siguiendo algún patrón de distribución, por arriba o por abajo, pero no de modo aleatorio como en la figura 2.
También podemos ver si tienen relación, con un test de correlaciones. Si vamos a Estadísticos/Resúmenes/Test de correlación y elegimos las variables T_1 y T_2 obtendremos la siguiente salida:
> with(pareados, cor.test(T_1, T_2, alternative="two.sided", method="pearson")) Pearson's product-moment correlation data: T_1 and T_2 t = 0.028577, df = 38, p-value = 0.9774 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.3073174 0.3156892 sample estimates: cor 0.004635723
La correlación es muy baja entre ambas 0,0046 y además no significativa (p-value = 0.9774. También podríamos haberlo visto yendo a Estadísticos/Resúmenes/Matriz de correlaciones y eligiendo nuestras variables T_1 y T_2 además de activar las observaciones a usar como Parejas de casos completos y aceptar la opción de obtener los p-valores pareados. Obtendremos:
> rcorr.adjust(pareados[,c("T_1","T_2")], type="pearson", use="pairwise.complete")
Pearson correlations:
T_1 T_2
T_1 1.0000 0.0046
T_2 0.0046 1.0000
Number of observations: 40
Pairwise two-sided p-values:
T_1 T_2
T_1 0.9774
T_2 0.9774
Si os ha surgido alguna duda durante la lectura y/o desarrollo de la actividad, no dudéis en contactar con nosotros y estaremos encantados de ayudaros.
Artículo número 176 publicado en Suis
Autores: Morillo Alujas, Alberto; Mehaba, Nabil; Nadal Zuferri, Sergio; Yagüe Utrilla, Gema; Villalba Mata, Daniel
Referencias
[1] Doménech, JM. (1996) Métodos estadísticos en Ciencias de la Salud. Ed. Signo. Barcelona. Capítulo 9 pág 38.