Interpretando los resultados de estudios
Artículo publicado en AviNews
Bradbury et al. 2017 publicaron un artículo en Animal Production Science, número 57, páginas 2016 a 2026, donde analizaron el efecto de una fuente de calcio muy soluble suplementada con fitasa en las dietas de pollos y estudiaron la digestibilidad de varios nutrientes, el contenido de cenizas, la movilidad de los animales y la debilidad de las patas.
No vamos a estudiar ni comparar este artículo o sus contenidos. Simplemente es un artículo que está publicado y lo hemos elegido como ejemplo para estudiar:
Cuáles deberían ser los datos que nos tiene que aportar una publicación,
qué nos dicen los diferentes resultados que se obtienen en los estudios y
cómo debemos interpretarlos.
Un artículo científico debería, además de informarnos de una serie de hallazgos que los autores han realizado con una experimentación, ser una guía que permitiera a otros investigadores, siguiendo los mismos métodos y con los mismos o parecidos materiales llegar (o no) a parecidas conclusiones que los autores del mismo.
¿En qué deberíamos fijarnos cuando leemos un artículo?
Bradbury et al. en la tabla 3 de su artículo nos informan del efecto de los niveles de fitasa entre los días 1 al 14 usando un diseño factorial 2x2x2 (dos fuentes de calcio, dos niveles de calcio y dos niveles de fitasa, ver tabla 1).
| Nivel de fitasa (FTU/kg) | Ganancia de peso (g/ave) | Consumo de pienso (g/ave) | Índice de conversión peso vivo/pienso (g/g) |
|---|---|---|---|
| 0 | 480 | 546 | 1,27 |
| 500 | 502 | 561 | 1,23 |
| Valor de P | < 0,001 | 0,01 | < 0,001 |
Tabla 1: Influencia de tratamiento dietético en los resultados productivos de pollos durante el periodo de 1 a 14 días de vida (modificado de Bradbury et al. 2017).
La media es un parámetro estadístico descriptivo de una población. Hay múltiples parámetros estadísticos descriptivos como la media, desviación típica, proporción, etc….. Al iniciar el experimento, los autores o nosotros mismos desconocemos el dato real de la ganancia de peso, del consumo y del índice de conversión de la población total de pollos (Cobb-500 en este caso). Lo que hacemos al elegir estos 1120 pollos del experimento, es tomar una muestra, y por tanto, estimaremos el valor del parámetro estadístico de interés, en este caso la media.
¿Tendríamos siempre los mismos resultados al hacer la prueba con una muestra de 1120 pollos Cobb-500?
Claro que no, pueden ser muy parecidos, pero no iguales. Por eso, el valor que obtenemos de una muestra se denomina estima de la media y como tal tiene un error asociado. El valor del estadístico (la media) de la muestra se utiliza para estimar el valor del parámetro desconocido de la población. Si las muestras son aleatorias, los estadísticos dan estimaciones puntuales no sesgadas de los parámetros correspondientes[1]. No obstante, como resultado, la estima puntual no nos da suficiente información sobre la prueba. Es imprescindible que cada estima (media, proporción, etc.) vaya acompañada siempre de su precisión (o de su error de estimación) que nos dará una idea de cuán buena es nuestra estima del valor verdadero, valor que nunca conoceremos.

Imaginemos…
…que repetimos el estudio de Bladbury y cogemos 1.120 pollos, los dividimos en dos grupos de forma aleatoria y obtenemos las ganancias de peso entre 1 y 14 días. Esto lo hemos simulado y hemos obtenido los siguientes resultados:
| Nivel de fitasa (FTU/kg) | Número de aves | Media de ganancia de peso (g/ave) | Desviación estándar (g/ave) | Error estándar de la media g(ave) |
|---|---|---|---|---|
| 0 | 560 | 477 | 35 | 1,48 |
| 500 | 560 | 500 | 39 | 1,64 |
Tabla 2: Simulación del experimento de Bladsbury
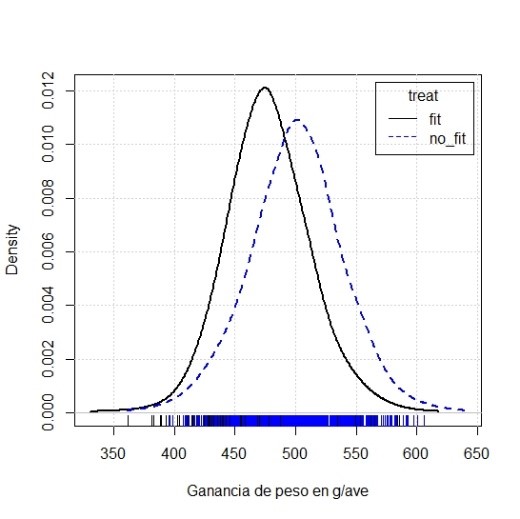
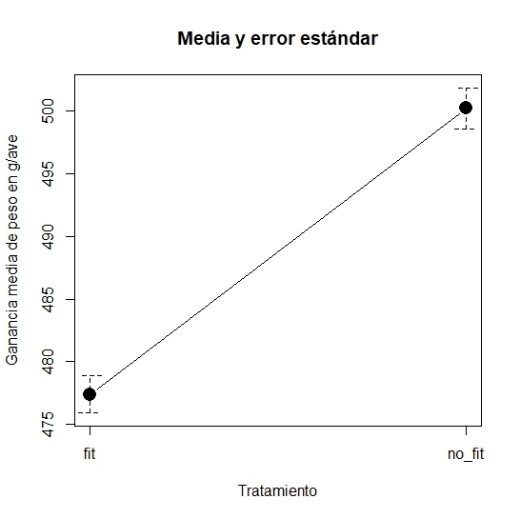
Tabla 3. Distribución de densidad de los tratamientos con y sin fitasa
La diferencia entre ambos tratamientos es 23 g/ave. En el experimento original la diferencia era de 22 g/ave muy cercano a nuestra simulación.
¿Qué es la desviación estándar?
Es un parámetro que describe la variabilidad de los datos y es necesario para conocer la precisión de nuestro muestreo. Como en el caso de la media, no conocemos la desviación estándar de la población, sino que la estimamos a partir de la muestra. Para el cálculo de la desviación estándar muestral se resta de cada uno de los valores de nuestro muestreo, la media estimada. Para que la suma de las diferencias no sea 0, elevamos al cuadrado esta diferencia. Finalmente dividimos por el número de datos “n” menos uno. Matemáticamente, su fórmula es:

Formalmente:

¿Qué es el error estándar de la media?
Si realizamos el muestreo aleatorio de cada grupo un número elevado de veces, de cada muestreo por individual, obtenemos una media.
- Estos valores no serán iguales entre ellos, y su variabilidad, medida como desviación estándar, es el error estándar de la media.
- Si medimos una variable con una variabilidad muy pequeña, (todos los pollos son iguales, desviación estándar muy baja) la variabilidad de las medias en diferentes pruebas también será pequeña.
- Si la variable medida tiene mucha variabilidad (desviación estándar alta) las medias de cada prueba también diferirán más.
Así, formalmente, el error estándar de la media (ESM) estimada en una población con desviación típica “s”, y un tamaño muestral “n”, es:
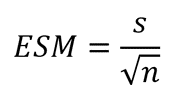
Si pensamos que nuestra variable aleatoria por el hecho de serlo sigue la famosa Ley Normal, el 95% de los valores de las ganancias de peso de los pollos dentro de cada uno de los grupos estará aproximadamente entre el valor de la media de su grupo y 2 veces (formalmente el valor es 1,96) el valor de la desviación estándar. Para ambos grupos:
| Nivel de fitasa (FTU/kg) | Intervalo de normalidad de la ganancia de peso (g/ave) |
|---|---|
| 0 | 477 ± 2 * 35 = 407 a 547 |
| 500 | 500 ± 2 * 39 = 422 a 578 |
Tabla 4. Intervalo de normalidad. Entre qué valores se encuentran el 95% de los pollos de la muestra
Y a este intervalo se le denomina intervalo de normalidad. Pero si lo que queremos conocer es la precisión de la muestra media, lo que debemos hacer es obtener el intervalo de confianza. En este caso se suma y se resta a la media 2 veces el error estándar de la media.
| Nivel de fitasa (FTU/kg) | Intervalo de normalidad de la ganancia de peso (g/ave) |
|---|---|
| 0 | 477 ± 2 * 1,48 = 474 a 480 |
| 500 | 500 ± 2 * 1,64 = 497 a 503 |
Tabla 5. Intervalo de confianza. Entre que valores se encuentra, con un 95% de confianza la media poblacional.
Y a este intervalo se le denomina intervalo de confianza del 95% de la media.
Si los valores de los intervalos obtenidos sin fitasa o con 500 FTU de fitasa no se superponen, intuitivamente ya podemos ver que la media del tratamiento sin fitasa estará por debajo de la media del tratamiento con 500 FTU de fitasa y, por tanto. atribuimos un efecto del tratamiento no debido al azar (estadísticamente significativo). También intuitivamente podemos ver que, conforme más estrecho sea cada uno de estos intervalos, el error de muestreo habrá sido más pequeño y tendremos, más confianza en nuestros datos.
¿Esta diferencia en los intervalos es importante?
En estadística, un resultado o efecto es estadísticamente significativo cuando es improbable que haya sido debido al azar. Una «diferencia estadísticamente significativa» solamente significa que hay evidencias estadísticas de que hay una diferencia; no significa que la diferencia sea grande, importante o radicalmente diferente. Esta diferencia nos la da el tamaño del efecto de la diferencia.
La diferencia estadísticamente significativa se define con un valor conocido como valor “p” y es la probabilidad estadística de obtener por puro azar, en este caso, una ganancia media de peso tan o más alejada de 477 g/ave (grupo sin fitasa) que la media de 500 g/ave (grupo con fitasa).
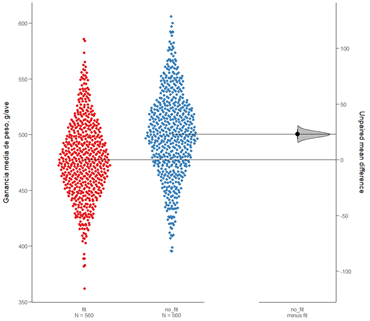
Tabla 6. Distribución y estimación del tamaño del efecto
¿Qué significa el 95%?
Si realizásemos nuestro muestreo de pollos 100 veces (1120 pollos tomados al azar 100 veces y someterlos a las mismas dietas), cada muestra nos daría una media y un intervalo de confianza. A la larga, el 95% de estos intervalos incluiría el verdadero valor medio de la ganancia de peso real, que nunca conoceremos. No podemos saber nunca si el intervalo obtenido en el experimento pertenece al 95% de los intervalos que incluye la media verdadera o al 5% restante que no: es el método el que acierta el 95% de las veces.
Así pues, al informar de los resultados de experimentos, los autores deberían darnos además de los estadísticos calculados (media, proporción…), el número de observaciones de cada conjunto de datos, su error estándar, su intervalo de confianza y el valor de la significación estadística.
Autores:
Morillo Alujas, Alberto ; Villalba Mata, Daniel ; Mehaba, Nabil ; Nadal Zuferri, Sergio

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional.
Referencias
[1] Domenech, J.M.1996. Métodos estadísticos en ciencias de la salud. Cap.5, 7.