Diferencia relevante y diferencia significativa

Un punto clave para el diseño de una prueba experimental que pueda someterse a un análisis estadístico es el cálculo del tamaño muestral.

«¿Cuál es el número de unidades experimentales (en nuestro caso animales, corrales, etc.) que se deben controlar para poder contestar, apoyados por un test estadístico, a la pregunta que nos lleva a realizar una prueba o experimento?». Este es un paso clave para el diseño de una prueba que pueda después ser analizada estadísticamente y de la que se puedan obtener unas conclusiones adecuadas.

En este post plantearemos el concepto de diferencia relevante y diferencia significativa, clave para continuar con el cálculo del tamaño muestral. Para ello es necesario introducir algunos conceptos previos.

Para el cálculo del tamaño muestral es necesario conocer la variabilidad de la población que utilizamos. Para la obtención de la varianza (medida de dispersión de la variabilidad) de la variable que analizamos tenemos dos posibilidades:

• Recurrir a la información de pruebas previas realizadas en las que se hayan tomado datos de la variable en cuestión. Ésta es la mejor metodología, especialmente si los datos provienen de animales lo más parecido posible a los que pretendemos analizar
• Buscar en la bibliografía pruebas lo más análogas posible y utilizar la variabilidad que hayan obtenido.

Supongamos que en nuestra base de datos, en el espesor de grasa dorsal (egd) tenemos que la media general es 16,4 mm y la varianza 10,415. La varianza es una medida muy utilizada para la dispersión, pero su raíz cuadrada, la desviación estándar, es más fácil de interpretar. En este caso, la desviación estándar de la muestra sería 3,227. En variables que se distribuyen siguiendo la función normal (que son las más típicas en producción animal), el 95 % de los animales tendrán valores entre aproximadamente dos veces la desviación estándar por debajo de la media y dos veces la desviación estándar por encima de la media.

Siguiendo el caso, los valores de egd para los animales deberían estar entre 9,9 (16,4 – 2*3,227) y 22,8 (16,4 + 2*3,3227).

El segundo concepto es que, en realidad, cuando hacemos una prueba tenemos una muestra de la población, y por tanto «estimamos» la media de la población a partir de la muestra que tenemos. Si la población tiene una dispersión pequeña (varianza pequeña), con pocos datos en la muestra, estimaremos bien la media. Si la población tiene una dispersión grande, harán falta mayor número de datos para estimarla bien. Esto es, cuantos más datos utilicemos, mejor estimada estará la media de la población. El parámetro que nos define lo bien o mal estimada que está una media es el error estándar de la misma:

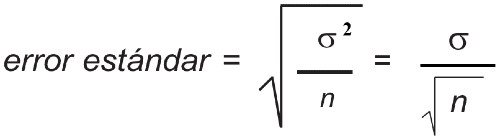
Aquí, σ² es el símbolo de la varianza, σ es la desviación estándar y n el número de datos de la muestra.

Cuando comparamos la media de dos muestras, estamos en realidad comprobando si las estimas de las medias son iguales o diferentes.

Supongamos un caso en el que estudiamos el egd en cerdas procedentes de dos muestras (ver siguiente gráfica). Nos podemos encontrar con dos casos extremos:

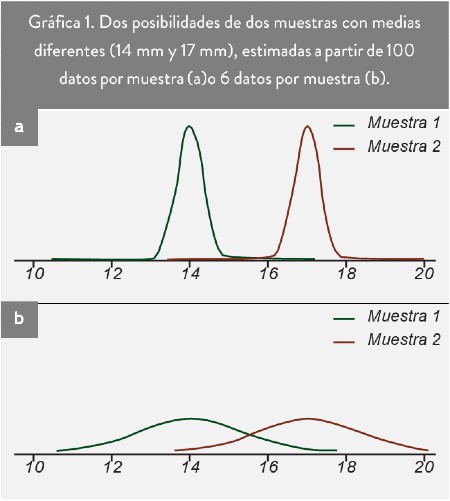
• El primero, la media de la muestra 1 es 14 mm, y la de la muestra 2, 17 mm; están estimadas con 100 datos por muestra, y el error estándar es 0,32 (gráfica 1a). Estamos bastante «seguros» de que la media es 14 y 17.
• En el segundo caso (gráfica 1b) las medias son las mismas, pero estimadas con sólo 6 datos por muestra; el error estándar es entonces 1,32 (estamos menos seguros de las medias, su distribución es más dispersa).

Gráficamente, cuando las dos medias solapan sus distribuciones (gráfica 1b) no podemos asegurar que las dos sean estadísticamente diferentes; si no se solapan (gráfica 1a) podemos asegurar que son estadísticamente diferentes.

En resumen, cuanto mayor sea el número de datos por muestra más «seguros» estaremos de la media que estimemos, y podremos demostrar estadísticamente diferencias más pequeñas entre medias. En un caso extremo, si tuviéramos 1.000.000 de datos, el error estándar sería tan pequeño que podríamos demostrar estadísticamente diferencias de 6 micrómetros entre medias.

Cuando tenemos que calcular el tamaño muestral es imprescindible definir cuál es la diferencia entre medias que consideramos relevante. Por ejemplo, en el caso de comparar las medias de espesor de grasa dorsal de dos piensos, ¿pretendemos demostrar diferencias de micrómetros o de mm? ¿Sería “relevante” desde el punto de vista comercial que un pienso nos proporcionara cerdas con un micrómetro más de egd, afectaría eso a los beneficios del ganadero?

Evidentemente, no.

Está claro que la diferencia relevante depende del nivel del estudio, de la variable que estamos analizando, incluso de la situación económica de la producción, pero no es menos claro que debe estar bien definido antes de comenzar el estudio.

Hemos visto que con un número suficiente de datos por muestra (por ejemplo animales por tratamiento) podemos demostrar que son significativas diferencias entre medias muy pequeñas, pero que no por ello son relevantes. Cuando observamos los resultados de un experimento podemos juzgar su diseño en función de estos dos términos. Por ejemplo, en el caso de la comparación de dos piensos y su efecto sobre el espesor de grasa dorsal de las cerdas, nos podemos encontrar con los siguientes resultados de diferentes experimentos:

Tabla: Ejemplos de experimentos bien (A y D) y mal diseñados (B y C)

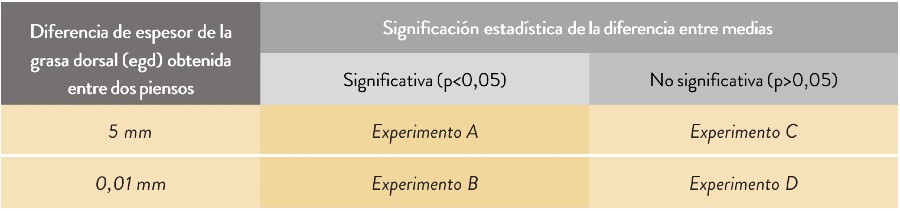
Los experimentos B y C se podrían considerar como errores de diseño: en el experimento B se ha escogido un tamaño muestral tan elevado que detecta diferencias no relevantes como significativas (hemos desperdiciado efectivos), mientras que, por otro lado, en el experimento C no detectamos una diferencia relevante (5 mm) probablemente debido a un tamaño muestral pequeño.

En cambio, los experimentos A y D se pueden considerar bien diseñados. En el primero, detectamos la diferencia relevante como significativa y en el segundo damos como no significativa una diferencia no relevante.

Conocer el mundo de la estadística y la producción es fundamental para diseñar buenos experimentos. Por ello, nuestro equipo cuenta con la formación y experiencia necesarios para realizar las pruebas con la máxima profesionalidad posible que garantice resultados fiables.

Para acceder gratuitamente a todos nuestros artículos de estadística publicados en los últimos 10 años, haz clic aquí.