¿Cómo comparar dos curvas de supervivencia?

En este artículo vamos a continuar con el tema introducido en el número anterior: Los análisis de supervivencia, donde terminamos generando dos curvas de supervivencia para dos grupos de cerdos, un grupo de cerdos vacunados y otro grupo control de cerdos tratados con placebo.

Observando las curvas del número anterior vemos que existen ciertas diferencias, pero ¿son estas diferencias significativas? A continuación, explicaremos cómo realizar este tipo de análisis.

Este tipo de contraste de hipótesis se puede resolver con un test Log-Rank para varios grupos. Este test se utiliza porque es capaz de comparar el número de eventos en cada grupo con el número de eventos que podría esperarse combinando ambos grupos.

El test Log-Rank es un test no paramétrico cuyo uso es apropiado cuando los datos pueden presentar censura por la derecha. Por esta razón, su uso en ensayos clínicos es muy común.

La fórmula del estadístico de Log-rank para comparar dos grupos es:

Siendo O los eventos observados y E los esperados. Como vemos, considera únicamente los datos de un grupo.

Si comparamos más de dos grupos, el estadístico del test Log-Rank se obtiene usando el cuadrado de la suma de las diferencias del número de observaciones menos el número que esperábamos dividido entre lo esperado. Para más de dos grupos, una aproximación válida sería utilizar un test chi-cuadrado. Sin embargo, siempre será más correcto determinar el estadístico Log-rank completo computacionalmente:

donde k = número de grupos

otros tipos de tests, como la prueba t de Student o la prueba de la suma de rangos de Wilcoxon, no son muy apropiados. Las razones son, por un lado, que nuestros datos no van a seguir una distribución normal y, como sabemos, es un requisito necesario para realizar una prueba t de Student. Por otro lado, en el caso del test de Wilcoxon, sí que lo podríamos utilizar como aproximación, pero debemos tener en cuenta que esta prueba no considera los datos censurados que caracterizan estos estudios de forma que los datos de fallos iniciales tendrán más peso que los datos de fallos posteriores.

Esto significa, a groso modo, que en los casos en los que un tratamiento tenga mayor efecto en las fases iniciales tras su administración, la prueba de Wilcoxon sí nos dará una aproximación válida. Aun así, como esto no siempre se cumple, recomendamos utilizar el test de Log-rank.

En este tipo de contrates de hipótesis, como podemos imaginar, se definen las siguientes hipótesis:

Para comenzar el análisis de las curvas con R-Commander, nos situamos en el punto donde lo dejamos en el número anterior, con los datos de ABRIL_BBDD VACUNA CERDOS.csv cargados (disponibles de manera totalmente gratuita). Una vez ahí, vamos a Estadísticos>Análisis de supervivencia>Comparación de las funciones de Supervivencia, tal y como se ve en la Figura 1.

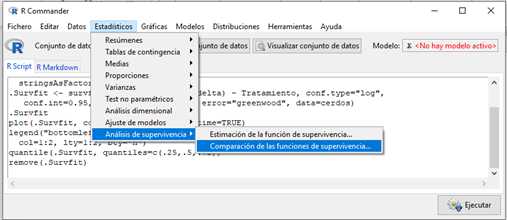
Figura 1. Ruta de acceso a la instrucción de comparación de funciones de supervivencia en R-commander.

Si ejecutamos las instrucciones, tendremos una salida correspondiente a los resultados del test como se muestra en la Figura 2.

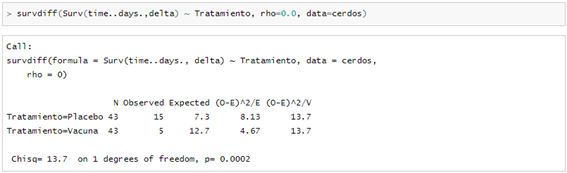
Figura 2. Output de R-Commander para el test Log-Rank comparando el grupo de cerdos placebo y el grupo de cerdos vacuna.

Obtenemos un p-valor=0.0002 para 1 grado de libertad ya que tenemos 2 grupos, por lo que tendremos evidencia estadística suficiente para rechazar H0 y, por tanto, asumir que las curvas y sus funciones son estadísticamente diferentes, tal y como ya se intuía con la representación gráfica.

La salida que aparece en esta imagen muestra los estadísticos de Log-rank.

Así pues, con la información recogida en las dos últimas publicaciones de esta sección, se espera que el lector sea capaz de realizar por sí mismo un análisis de supervivencia usando R-Commander, obteniendo y comparando las funciones de las curvas de supervivencia de dos grupos de los que se pretende estudiar si hay diferencias o no en la respuesta en el tiempo a un posible tratamiento.

Artículo nº178 de Suis