¿Cómo determinamos el efecto que tiene sobre la ganancia media diaria de los lechones incluir en la dieta harina de pescado en diferentes cantidades?
Un estudio estadístico a menudo compara más de dos poblaciones. Por ello, la Estadística incluye métodos específicos para comparar cualquier número de medias y ser útil en cualquier contexto. Para clarificar, veamos un ejemplo de comparación de dos medias y otro de comparaciones múltiples:
- Comparación de dos medias: Evaluar el efecto de incluir harina de pescado en la dieta de los lechones en la ganancia media diaria de estos. En este caso, evaluamos el efecto de una variable sobre la media de otra variable.
- Comparación múltiple: Evaluar el efecto de incluir en la dieta harina de pescado en diferentes cantidades en la ganancia media diaria de estos.
En este post, vamos a resolver a la pregunta título que responde a un caso de comparación múltiple: ¿Qué análisis utilizamos para determinar el efecto que tiene, sobre la ganancia media diaria (GMD, en adelante) de los lechones, incluir en la dieta harina de pescado en diferentes cantidades?
Comenzamos
Supongamos que se han distribuido tres dietas a 20 lechones en la etapa de prestarter:
- La dieta 1 contenía un 0% de harina de pescado.
- La dieta 2 contenía un 4% de harina de pescado.
- Por último, la dieta 3 contenía 8% de harina de pescado.
Los resultados obtenidos en cuanto a ganancia media diaria fueron los siguientes:
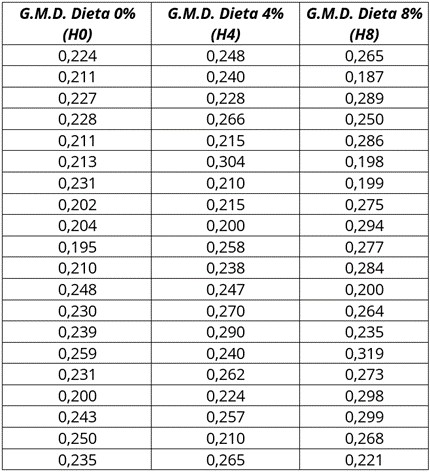
Tabla 1: Ganancia Media Diaria según cantidad de harina de pescado incluida en la dieta
En primer lugar, vamos a explorar nuestros datos y extraer algunos estadísticos básicos (para este ejercicio, nosotros vamos a utilizar el programa Síagro):
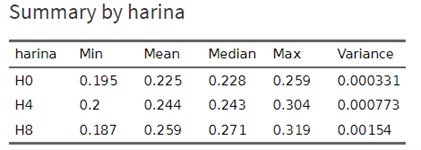
Tabla 2: Análisis Exploratorio
Como podemos comprobar la media de la GMD aumenta a medida que también lo hace el contenido de harina de pescado de la dieta de los lechones: la media de la GMD para la dieta con 0% de harina de pescado es de 0,224, para la dieta de 4% es de 0,244, y que para la dieta de 8% es de 0,259. Ahora, la pregunta que nos deberíamos hacer es la siguiente, ¿son estadísticamente significativas estas diferencias?
La problemática de las comparaciones múltiples
Antes de nada, empecemos dando nombre a las medias de las GMD de los lechones. Para la dieta con 0% de harina de pescado la media será m1, para la dieta con un 4% de harina de pescado la media la llamaremos m2, y para la dieta con el 8% de harina de pescado la media será m3.
Si pretendemos comparar estas tres medias podríamos usar varias veces la prueba t de dos muestras, pero esto es una pérdida en tiempo innecesaria, ya que tenemos modelos Estadísticos específicos para para contexto. De todas maneras, explicamos al final del post cómo podríamos hacerlo por si el lector quiere indagar más.
Además, el inconveniente que nos encontraríamos al hacer estas tres pruebas es que obtendríamos tres valores P, uno para cada prueba. Esto no nos dice cuál es la probabilidad que otras tres medias muestrales cualquiera estén tan separadas como éstas. Es decir, puede ser que m1 y m3 sean estadísticamente distintas si nos fijamos en la comparación de estas dos medias, pero podría ser que no fueran estadísticamente distintas si sabemos que son la media menor y mayor de los tres grupos. En conclusión, no podemos comparar, de una manera categórica y mediante pruebas de significación, muchas medias de dos en dos.
El problema de comparar varias medias conjuntamente puede resolverse mediante un Análisis de Varianza o ANOVA (por sus siglas en inglés de Analysis of Variance).
Su dificultad es mínima, aunque mayor que en el caso de los contrastes de significación. Como veremos, estas pruebas nos permiten comparar todas las medias conjuntamente y nos permitirán discernir si hay diferencias significativas entre todas las medias. Una vez detectadas diferencias entre ellas, en un análisis posterior, podremos determinar las diferencias entre cada una de las medias por separado. Este último análisis se realizaría con programas estadísticos especializados como podrían ser los llamados tests de Duncan, tests de la Mínima Diferencia Significativa, etc.
Análisis de Varianza de un factor. Prueba F del Análisis de varianza
Una singularidad de la estadística es que uno de los métodos para poder comparar medias se denomine Análisis de la Varianza (ANOVA, en adelante). El motivo es que esta prueba se lleva a cabo comparando dos tipos de variación. El ANOVA es un método general para estudiar las fuentes de variación en las respuestas. La comparación de varias medias se llama Análisis de Varianza de un factor. Es de un factor debido a que la variable respuesta, en nuestro ejemplo GMD de los lechones, sólo se ve influida por otra variable, en nuestro ejemplo, el contenido de harina de pescado en la dieta. La prueba más sencilla del Análisis de Varianza para comparar varias medias se denomina prueba F.
El estadístico F utilizado para comparar varias medias tiene la siguiente forma:
F = variación entre medias muestrales / variación entre individuos de la misma muestra
El estadístico F sólo puede tomar valores positivos o cero. Será cero cuando las medias sean todas iguales. De hecho, el efecto del azar crea algunas diferencias entre las medias muestrales, aun cuando las medias de las poblaciones son iguales. Así, cuando la hipótesis nula es cierta, esperamos que F tome valores próximos a uno. A medida que las medias muestrales están más separadas entre sí, el valor de F se hace mayor.
Los valores grandes de F constituyen una prueba fehaciente en contra de la hipótesis nula, inclinándonos a pensar que la hipótesis correcta es la alternativa, la que contempla que alguna de las medias muestrales no es igual a las demás.
No hay una mejor explicación que la que se pueda ver en un ejemplo
De esta manera, sigamos el hilo del ejemplo que planteamos en la introducción. Queremos contrastar la hipótesis nula de que no existen diferencias entre la GMD de los lechones para las tres dietas con diferente contenido en harina de pescado. Es decir:
- H0: m1 = m2 = m3
La hipótesis alternativa plantea que sí existe alguna diferencia entre las medias, es decir, no todas las medias son iguales:
- Ha: m1 ¹ m2 ¹ m3
La Ha contempla el caso que m1 = m2, pero que m3 tenga un valor diferente, o cualquier otra combinación. El contraste de H0 contra Ha se denomina prueba F del ANOVA.
Análisis de la Varianza en Síagro
Para proseguir con el ANOVA del ejemplo debemos utilizar el programa Síagro (pueden utilizar R, pero les avisamos les llevará mucho más tiempo). Una vez introducidos los datos del ejemplo, entraremos en la opción Modelos de Predicción, que estará siempre por defecto en el panel de control, e iremos a ANOVA.

Figura 1. Acceso a ANOVA en Síagro
A continuación, seleccionaríamos la variable GMD y el factor harina. En la primera, si observamos, disponemos de los datos recogidos en campo y, la segunda, los tres factores: H0, H4 y H8.
El resultado de realizar esta operación es el siguiente:

Donde:
- Df: grados de libertad
- Sumsq: suma de cuadrados
- Meansq: Promedio de cuadrados
- Statistic: Estadístico de contraste F
- P-value: Probabilidad
Y,
- Harina: Entre grupos
- Residuals: Dentro de los grupos
Fijémonos principalmente en el estadístico de contraste F, F = 6,81. Como dijimos, un mayor valor de F nos daba una idea que la hipótesis nula no era la correcta. Ahora observemos su probabilidad (p-value), que es de 0,00223. Mientras el valor de la probabilidad se sitúe por debajo de 0,05 (el nivel de significación tradicionalmente aceptado), podremos afirmar que existe la evidencia de que los tres tipos de dieta no son iguales, o alguna de las tres dietas es diferente a las demás, es decir, afectan de forma diferente a la Ganancia Media Diaria de los lechones. Estamos en disposición de rechazar la hipótesis y aceptar como cierta la hipótesis alternativa.
La prueba F del ANOVA valora la evidencia de que existe alguna diferencia entre las medias poblacionales.
En la mayoría de los casos siempre esperamos que esta prueba sea significativa. No emprenderíamos el estudio posterior, comparar una a una cada media, si no encontrásemos diferencias. Si bien parece contradictorio a lo que se ha dicho en el apartado anterior, y debido a que los programas estadísticos no están al alcance de todos, no sería descabellado que, una vez realizada la prueba F, separáramos cada una de las medias mediante contrastes una a una. Eso sí, tendremos que ser conscientes que en cada prueba posterior que realizamos tenemos una probabilidad de error del 5% (si comparamos 7 medias dos a dos en al menos una cometeremos el error de aceptar la Hipótesis alternativa cuando no es cierta).
La prueba F nos sirve como precaución para evitar ser engañados por las variaciones debidas al azar.
Análisis de Varianza de varios factores
Como hemos estado viendo en el ejemplo, el único factor que podía perturbar a nuestra variable respuesta, la Ganancia Media Diaria, era el contenido de harina de pescado de la dieta. Este es el caso más sencillo que nos podemos encontrar cuando analicemos unos datos y deseemos comparar medias. Planteemos otra cuestión…
¿Qué hubiese sucedido si hubiéramos separado a los lechones en dos mitades y les hubiéramos suministrado dos dietas diferentes en energía, a parte del contenido de harina de pescado?
La variable Ganancia Media Diaria ya no sólo estaría influenciada por el factor contenido en harina de pescado, sino que también lo estaría o podría estarlo por la cantidad de energía que aporta la dieta. De hecho, el nivel de factores puede ser muy amplio, pero entonces el análisis se complicaría de forma exagerada.
Prueba T de dos muestras
Como habíamos introducido al inicio del artículo, por si el lector quiere indagar más, presentamos la realización de varias pruebas T de dos muestras. Antes de nada, debemos aclarar que para realizar los siguientes cálculos ha sido necesaria realizar una corrección (un Welch’s t-test). El Welch’s t-test se realiza cuando la prueba de homogeneidad de varianzas nos indica que las varianzas no son homogéneas y, por tanto, no podemos suponer que un T-test sin corrección es correcto.
Comenzamos el análisis:
Contrastando, H0: m1 = m2
Ha: m1 ¹m2
obtendríamos,
| Prueba t | ||
| Dieta 0% | Dieta 4% | |
| Media | 0,224597273 | 0,244409508 |
| Varianza | 0,000332316 | 0,000772273 |
| Observaciones | 20 | 20 |
| Diferencia hipotética de las medias | 0 | |
| Grados de libertad | 33 | |
| Estadístico t | -2,665925185 | |
| P(T<=t) una cola | 0,005897692 | |
| Valor crítico de t (una cola) | 1,692360456 | |
| P(T<=t) dos colas | 0,011795385 | |
| Valor crítico de t (dos colas) | 2,03451691 |
- Contrastando, H0: m1 = m3
Ha: m1 ¹m3
obtendríamos,
| Prueba t | ||
| Dieta 0% | Dieta 8% | |
| Media | 0,224597273 | 0,259078641 |
| Varianza | 0,000332316 | 0,001545718 |
| Observaciones | 20 | 20 |
| Diferencia hipotética de las medias | 0 | |
| Grados de libertad | 27 | |
| Estadístico t | -3,558342376 | |
| P(T<=t) una cola | 0,000702746 | |
| Valor crítico de t (una cola) | 1,703288035 | |
| P(T<=t) dos colas | 0,001405491 | |
| Valor crítico de t (dos colas) | 2,051829142 |
- Contrastando, H0: m2 = m3
Ha: m2 ¹m3
obtendríamos,
| Prueba t | ||
| Dieta 4% | Dieta 8% | |
| Media | 0,244409508 | 0,259078641 |
| Varianza | 0,000772273 | 0,001545718 |
| Observaciones | 20 | 20 |
| Diferencia hipotética de las medias | 0 | |
| Grados de libertad | 34 | |
| Estadístico t | -1,362584789 | |
| P(T<=t) una cola | 0,090985713 | |
| Valor crítico de t (una cola) | 1,690923455 | |
| P(T<=t) dos colas | 0,181971426 | |
| Valor crítico de t (dos colas) | 2,032243174 |